






人的行动是在社会中进行的。但个人决策的基本原理甚至整个社会的基本经济问题都可以通过对一个孤立的个体的经济行为的分析得到。经济学家喜欢用鲁滨孙·克鲁斯的故事来讨论一个人既是消费者又是生产者的情形。鲁滨孙·克鲁斯是英国小说家丹尼 尔·笛福的《鲁滨孙漂流记》中的主人公,因出海遇险,漂流到一个荒无人烟的小岛上,并坚持在岛上生活若干年,最后回到文明社会。
鲁滨孙经济: 生产者和消费者合二为一的个体经济,没有交换介入。
流落到荒岛上的鲁滨孙需要解决生存问题:如果没有食物,他很快就会饿死。好在岛上有丰富的自然资源,例如有好多的椰子树,椰子可以用来充饥。但要把椰子从树上摘下来,需要花费劳动。鲁滨孙面对的约束就是他的时间有限,一天总共24个小时,他要劳动也要休息。鲁滨孙的决策就是如何分配时间,如果他花更多时间去摘椰子,那就必须减少休闲的时间,睡觉就得少一点。经济学把能够直接带来快乐的时间称为休闲。一项行动属于休闲还是劳动,与肢体运动无关。例如人们下班后去卡拉OK唱歌,满头大汗,但觉得快乐,这就属于休闲。站岗的武警在那儿站着几个小时动都不动,却属于工作,不是休闲,因为这个过程没有给他带来快乐。经济学有关劳动和休闲的定义的划分,就在于人们行动的主要目的是过程本身还是获得的结果。当然在现实中,二者很难严格区分。
表2-2给出了鲁滨孙工作1~11个小时对应的总产量、总效用和总成本,以及对应的边际效用和 边际成本 。这里,产量按椰子的个数计算,效用指消费椰子带来的满足,成本是指劳动带来的负效用(也即减少休闲所带来的效用损失)。边际效用和边际成本分别表示增加1单位产品(椰子)对应的效用增加值和成本增加值。从这个表中我们看到,椰子本身是好东西(good),因此多多益善,即总效用数值随着椰子产量的上升而上升。同时,劳动本身是坏东西(bad),以效用损失衡量的为生产椰子放弃的休闲时间的成本,也是椰子产量的增函数。不过二者对应的边际数值呈现出增减不一致的情况。边际效用随着椰子产量的增加而递减,边际成本随着椰子产量的增加而递增。
边际成本: 增加一单位产品的生产( 或消费)所付出的代价或放弃的收益。
表2-2 椰子生产的效用和成本
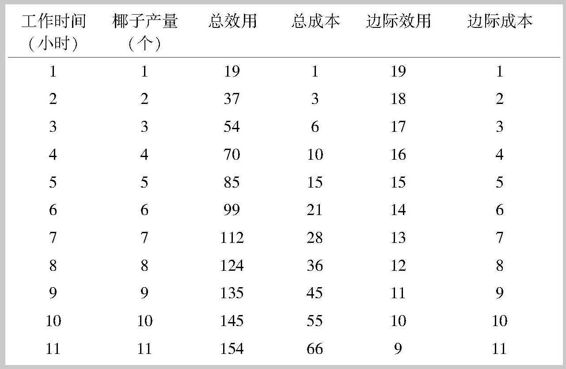
边际效用随产量的增加而递减来自我们上一节讨论过的“边际效用递减法则”。为什么边际成本会递增呢?有两个可能的原因:第一,随着产量的增加,采摘更多的椰子变得越来越困难(理性的鲁滨孙一定会从最容易采摘的椰子开始采摘);第二,随着劳动时间的增加,单位劳动时间的疲劳程度会随之增加(包括体能的消耗和厌烦),或者说随着休闲时间的减少,单位时间休闲的价值越来越高。
第一个原因被称为“边际生产率递减法则”,我们将在后面的章节中讨论。在上面的例子中,我们假定不论劳动时间多长,多工作1个小时就可以多采摘1个椰子,即鲁滨孙的劳动生产率是不变的,实际排除了第一个原因。现实中,这个原因是很重要的。
鲁滨孙应该花费多少工作时间采摘多少椰子呢?从表2-2中可以看出,他应该会选择花10个小时采摘到10个椰子。原因就在于,该产量值对应的边际效用等于边际成本,从而恰好使得他的净效用最大化。实际上,以幸福为目的的决策人最关心的既不是总收益,也不是总成本,而是净收益(或净效用)的大小。在这个例子中,总收益表示为总效用,净收益由总效用减去总成本得到,边际净收益(即每增加1单位椰子带来的净效用的变化)等于边际效用减去边际成本。当椰子产量少于10个时,边际效用大于边际成本,此时增加椰子产量会使净收益增长。当椰子产量大于10个时,边际效用小于边际成本,此时降低椰子产量会使净收益增长。只有在椰子产量为10个时,无论增加还是减少椰子的产量都不能使净收益变大了,因此实现了净收益目标的最大化。
一般地,我们有如下最优决策规则:
最优决策规则 最优选择在边际效用等于边际成本时达到。
图2-2给出了更为直观的描述。图中我们分别画出了边际效用曲线和边际成本曲线。当椰子产量等于10个的时候,边际效用等于边际成本,净收益达到最大。
图2-2 边际效用和边际成本
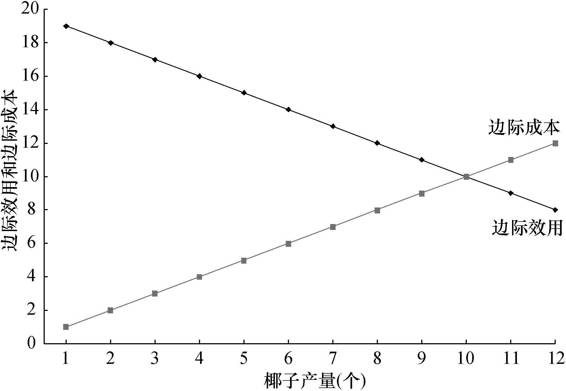
图2-3描述的是更为一般的情况。图中,横坐标代表产量(或劳动时间),纵坐标表示总效用和总成本。总效用曲线和总成本曲线之间的距离代表净收益。总效用曲线的斜率是对应产量下的边际效用,总成本曲线的斜率是对应产量下的边际成本。最优产量在净收益最大点达到,此时,总效用曲线的斜率和总成本曲线的斜率相等,也即边际效用等于边际成本。
图2-3 总效用和总成本
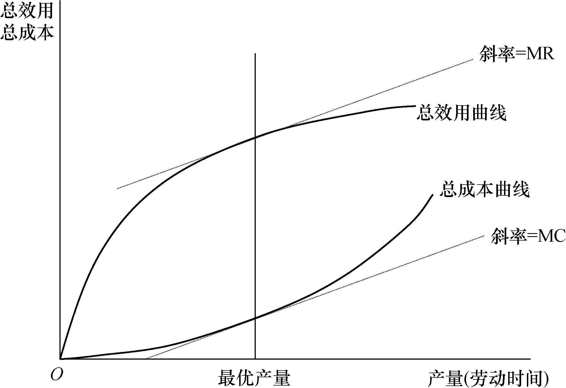
最优产量在总效用曲线和总成本曲线之间的距离最大时达到,此时边际效用等于边际成本。

上面例子讲述了鲁滨孙在椰子和休闲两种消费上的决策。就一天的事务而言,工作10个小时采摘10个椰子,把余下的14个小时用于休闲(包括睡眠)是合适的。但考虑到自己被困在孤岛上的时间可能会很长,鲁滨孙不得不有更长的视野。如果某一天自己生病了不能采摘椰子了该怎么办?他会想到自己应该有点积蓄。他还可能想到,或许应该花点时间造一个杆子,这样,花同样的时间就可以采摘更多的椰子。但造一个杆子也需要花时间,或者得减少采集的时间,或者得减少休闲的时间。
有了这些考虑,鲁滨孙会认识到,把10个椰子都吃掉并不是最好的选择。假定他决定吃掉8个椰子,把另外的2个储存起来。这样的话,按照经济学的术语,鲁滨孙一天的收入是10个椰子,其中8个椰子用于当期的消费,2个椰子变成储蓄。在经济学中,储蓄总是等于收入与消费之差,即 储蓄 = 收入 - 消费 。
收入: 一定时期内生产的可用于消费和投资的产品总量。
消费: 直接满足个人偏好的产品消耗。
储蓄: 为了投资和防患于未然而不用于消费的收入。
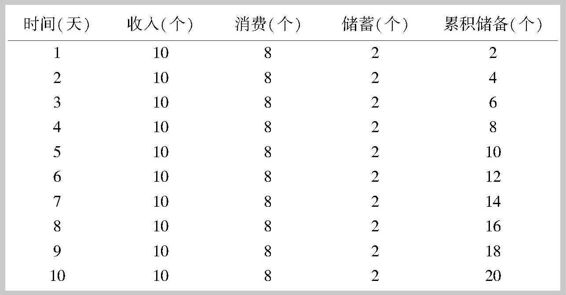
假定鲁滨孙一直没有生病,这样到第十天结束的时候,他已经积累了20个椰子了(见表2-3),这意味着他一天不工作也不会挨饿了。但他知道,如果制作一个杆子就可以提高摘椰子的效率,使得每小时工作可以摘到2个椰子。所以,他决定在第十一天花10个小时制作工具——杆子,而不是继续摘椰子。在经济学上,这个杆子,就是作为 生产要素 的 资本品 。
资本品: 人创造的、不能直接由大自然赐予的生产要素。
生产要素: 生产产品所需要的各种投入,包括劳动、资本品、土地和其他自然资源。
表2-3 杆子制作前的情形
再假定,预期到从第12天起,由于有了新的生产工具,每天工作10个小时可以采摘到20个椰子,收入(产量)比原来翻了一番,鲁滨孙决定在第11天把积累的20个椰子吃掉10个,并且从第12天开始,每天吃15个椰子,储蓄5个。表2-4给出从第11天开始鲁滨孙的经济境况。到第21天的时候,他的总储蓄达到60个椰子,活得更踏实了。
投资: 将储蓄转化为资本品的活动,目的是提高未来的生产率。
本例中杆子就属于资本品。制作杆子的过程可以看作通过消耗储蓄的椰子来换取生产能力的提高,即“投资”。
表2-4 杆子制作时与制作完成后的情形
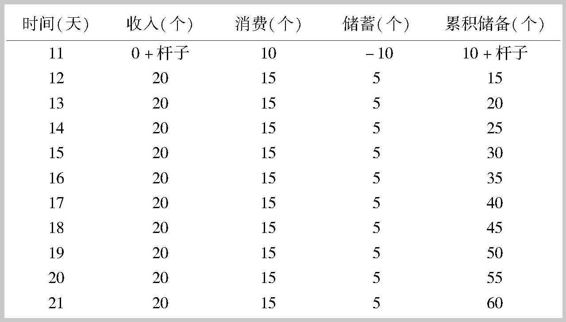
不过,杆子在使用过程中是会发生磨损的。在经济学上,这种磨损被称为资本品的“ 折旧 ”。
折旧: 资本品在使用过程中因磨损导致的价值损失。
假定杆子最多只能用10天。那么到了第22天,鲁滨孙又需要决定是否再生产一个杆子了。由于此时积累的椰子数量达到60个,他既可以按照第11天的情形,在第22天制作出同样一根杆子(等同于修复旧杆子),也可以选择花更长的时间(2天),做一个更大的投资——生产一个更高质量的杆子,这个高质量的杆子可以让鲁滨孙1个小时摘到5个椰子。如果选择后者,由于工作效率的提高,鲁滨孙从第24天开始可以将工作时间减少到每天6个小时,采摘到30个椰子,这不仅增加了休闲时间,同时还可以把每天消费的椰子增加到24个,储蓄增加到6个。表2-5和表2-6给出了这两种情形的对比。
表2-5 简单重复生产一根杆子的情形
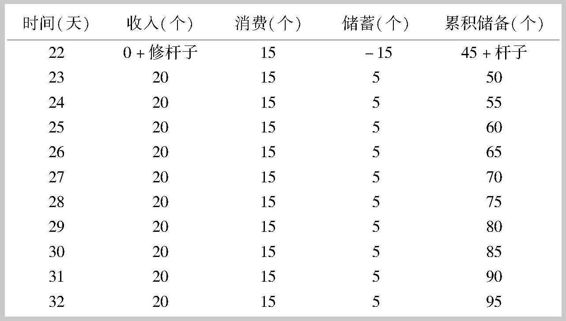
表2-6 生产出更高质量杆子的情形
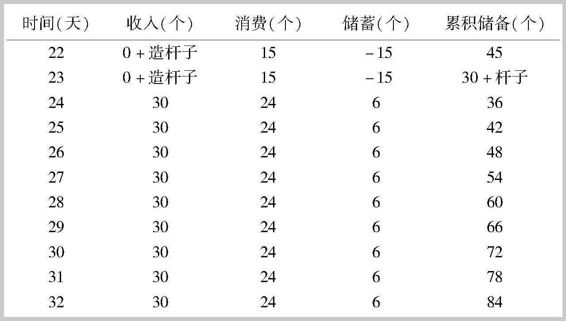
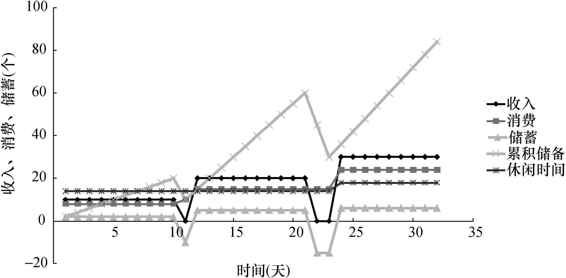
假定权衡之后,鲁滨孙决定选择后者。这个新的高质量杆子花了2天时间,在制造的时候其价值等于40个椰子。无论从收入、消费、财富(总储蓄)、资本品哪一方面衡量,鲁滨孙的经济状况都大大改进了。这就是经济学家讲的 由资本积累(投资)导致的经济增长 。图2-4给出了鲁滨孙生活变化的轨迹。
经济增长: 单位时间内生产率的提高和可用于消费的产品的持续增加。
图2-4 鲁滨孙的生活变化
在前面的讨论中,我们在计算鲁滨孙的收入时,只计算了每天生产的椰子的数量。由于这个原因,当他花时间制造杆子即从事投资活动时,他当期的收入为零、储蓄为负,累计储蓄也下降了。但按照现代经济学的定义,资本品的价值也应计算在收入之内。这样,在第11天制造第一个杆子的时候,他当期的收入应该是相当于10个椰子(即杆子的价值等于10个椰子,因为如果他不制造杆子,同样的时间可以采摘10个椰子),他的储蓄是零;在第22天和23天制造第二个杆子的时候,他每天的收入相当于20个椰子,每天的储蓄是5个。
另外,鲁滨孙也不一定集中时间制造杆子。比如说,他可以从第一天开始每天花1个小时制造杆子、9个小时采摘椰子,这样到第10天的时候他就有了生产工具。他也可以从开始使用杆子的那天起每天从采摘中抽出1个小时维修杆子,这样到第21天时杆子仍然完好如初。此时,每天1个小时相当于补充资本品的折旧。
在现代经济学中,储蓄的椰子算作“存货投资”,所以“储蓄”总是等于“投资”。