





如果一个人不是数学家,当他听说“四维”事物时会产生一种惊异感,觉得这是一件不可思议的神秘事情。但是,我们生活的世界就是个四维“空间—时间连续区”,这是真实存在的事情。
空间是三维连续区,这句话的含义是,对于一个处于静止状态的点来说,可以用 x 、 y 、 z 三个坐标去表示它的位置,同时,在这个点的周围存在着无数个不确定的点,可以用 x' 、 y' 、 z' 去描述这些点,这些坐标的值非常接近第一个点的坐标 x 、 y 、 z 的值。由于这些值非常接近,我们认为这个区域是“连续区”。由于需要三个坐标去表示,所以我们认为它是“三维”的。
同理,闵可夫斯基把空间—时间观简称为“世界”,这个物理现象肯定是四维的。所有的事件一起构成了物理现象的世界,而每一个事件的描述都需要使用 x 、 y 、 z 三个空间坐标和 t 一个时间坐标。这个“世界”同样是一个连续区,只要确定了一个事件之后,我们就可以为它任意选取“毗邻”事件 (感觉到的或者设想到的) 。这些事件的坐标 x' 、 y' 、 z' 、 t' 和最初确定的坐标 x 、 y 、 z 、 t 有一定的差值,根据经典力学的理论可以得知,这表明时间是绝对的,即时间与坐标系的位置不受运动状态的影响。我们明白,伽利略变换方程中的最后一个方程( t' = t )体现了这一点。
在相对论中,总是用四维方式来观察这个“世界”,因为相对论观点让时间不再具有独立性。这一点由洛伦兹变换方程中的第四个方程表现出来:
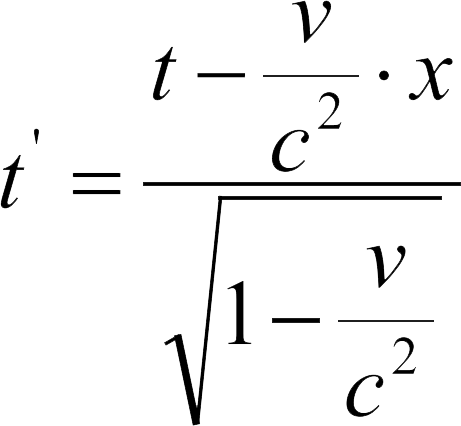
此外,根据这个方程可以得知,如果两个事件相对于 K 的时间差是 t ,当 t' =0时,两个事件相对于 K' 的时间差不一定是零。两个事件相对于 K 的“空间距离”转化成了这两个事件相对于 K' 的“时间距离”。对于相对论来说,闵可夫斯基的发现有着重要的意义。此外,闵可夫斯基发现,在某些方面,相对论的四维空间—时间连续区和欧几里得空间的三维连续区有着紧密的关系。为了说明这个关系,我们引入一个虚量ict去替换时间坐标,通常它和时间坐标是正比关系。于是,我们用数学形式表示符合相对论要求的自然定律的时间坐标和三个空间坐标。在形式上,这四个坐标和欧几里得几何学中的三个空间坐标完全相等。即使不是数学家的一般人也会发现,这个形式让相对论变得容易理解一些。
通过上面的内容,大家对闵科夫斯基的贡献有了一个模糊的认识。如果没有闵可夫斯基的贡献,广义相对论的基本观念也许永远无法挣脱襁褓的束缚。不了解数学的人难以理解闵可夫斯基的学说,但要理解狭义相对论或者广义相对论的基本观点,无需深入理解闵可夫斯基的学说,现在我先说这些,在这本书的第二部分结束时我会再次谈论这个问题。
如果把时间变量
t
替换为假定的
 ,我们可以更加简便地阐释洛伦兹变换方程的特征。同理,如果我们引入
,我们可以更加简便地阐释洛伦兹变换方程的特征。同理,如果我们引入
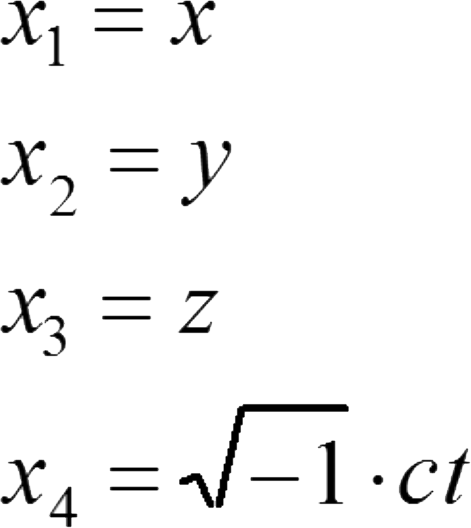
用类似的方式表示带有重号的坐标系 K' ,那么,为了让洛伦兹变换公式相等,必须有一个前提条件:
x ' 1 2 + x ' 2 2 + x ' 3 2 + x ' 4 2 = x 1 2 + x 2 2 + x 3 2 + x 4 2 (12)
借助于上述“坐标”,公式(11b)转换成了公式(12)。
在公式(12)中,通过相同的方式,虚构的时间坐标 x 4 进入空间坐标 x 1 、 x 2 、 x 3 中。由此可知,根据相对论的观点,“时间”坐标 x 4 和空间坐标 x 1 、 x 2 、 x 3 通过相同的形式表示自然界中的定律。
通过“坐标” x 1 、 x 2 、 x 3 、 x 4 描述闵可夫斯基简称为“世界”的四维连续区,他把表示某个事件的点叫做“世界点”。这样一来,根据物理学中的说法可知,可以用四维“世界”中的“存在”去表示三维空间中的“事件”。
这个四维“世界”和 (欧几里得) 解析几何学中的三维“空间”非常相似。如果我们在“空间”中引入一个具有同一原点的新的笛卡尔坐标系( x 1 、 x 2 、 x 3 ),那么,新的 x 1 、 x 2 、 x 3 就是原来的 x 1 、 x 2 、 x 3 的线性齐次函数,并且和方程 x ' 1 2 + x ' 2 2 + x ' 3 2 = x 1 2 + x 2 2 + x 3 2 相等。
这个完善的方程类似于公式(12)。在形式上,我们可以认为闵可夫斯基“世界”类似于 (假想时间坐标) 四维欧几里得空间和洛伦兹变换的坐标系的“转动”。
四维空间也叫做“四度空间”“四度时空”“四维宇宙”“时空连续区”等。通过一般的三维空间和时间一起构成。由于这个概念是德国的数学家闵可夫斯基提出的,所以又被称为“闵可夫斯基时空”。为了确定所有的物理事件,需要用三个空间坐标和一个时间坐标进行描述,这四个坐标共同构成了“超时空”,也就是所谓的“四维空间”。
(1)狭义相对论的思想可以用相对性原理和光速不变原理概括。
相对性原理:一切惯性参考系都是等价的,或者说对于所有的惯性系来说,物理规律都可以用相同的形式去表示。
光速不变原理:在真空中,光相对于任何惯性系的任意方向的传播速度永远是c。
(2)狭义相对论的理论核心通过洛伦兹变换方程来描述。
(3)狭义相对论有运动尺度缩短、运动时钟延缓、同时的相对性三个效应。
(4)狭义相对论中的其他内容:运动质量变大、速度相加定理、质能转换关系、能量—动能关系、作用的讯号与最大传播速度因果律,等等。
(5)狭义相对论的适用范围是高速(可以和光速相互比较)运动的物体,低速运动的物体符合经典力学中的运动定律。前面讨论的问题的错误之处在于,用经典力学中的伽利略变换分析高速问题,所以才会得出“不同坐标系中的物理规律不同”的错误结论。
狭义相对论被各个方面的经验所证实,已经成为现代物理学的理论基础。它为深入探索经典物理和量子理论奠定了基础,尤其是在研究基本粒子理论和宇宙奥秘时有着重要的作用。
斯蒂芬·茨威格在《人类群星闪耀的时刻》这本广为流传的小册子中说:“这是一个对于世世代代的人来说都有着重要意义的时刻,它决定着一个人的生死、一个民族的存亡,甚至是整个人类的命运。”在他眼中,一个个的伟大人物和一刻刻的重要瞬间组成了历史,而其他的时间只是准备阶段而已。因此,如果让斯蒂芬·茨威格来记载20世纪的历史,他一定会把1905年当作起点,人类群星中最耀眼的一颗星在这一年射出万丈光芒。
1905年,爱因斯坦只有26岁。如果我们不知道这个年轻人是爱因斯坦,那么,我们绝对相信这个不幸的年轻人在人生问题上是个失败者:中学辍学;在第二次投考中终于考上苏黎世联邦技术大学;虽然数学成绩和物理成绩很不错,但综合成绩中等的他失去了留校任教的资格;提交给苏黎世联邦技术大学的论文没有通过。由于父亲的企业破产,爱因斯坦的生活受到严峻的考验。他担任过中学教师、辅导教师等职务。在朋友格罗斯曼的帮助下,他在伯尔尼专利局得到一份稳定的工作,开始过着小职员的生活。他有一个善解人意的妻子和两个活泼可爱的孩子。
伯尔尼专利局的局长弗里德里希·哈勒是一个物理爱好者,他是第一个欣赏爱因斯坦的人。他给了这个面临生计困难的年轻人一份稳定的公务员工作和一份相当不错的薪水。爱因斯坦在伯尔尼专利局工作的时间长达七年,这段时间是他在学术生涯中思维最活跃、精力最集中的时期。
其中的1905年,不仅是爱因斯坦的“奇迹年”,也是物理学史上的第二个奇迹年。1655年是物理学史上的第一个奇迹年,牛顿在这一年开始思索微积分、万有引力定律、颜色理论。1905年,爱因斯坦在德国著名的物理学期刊《物理学纪事》中发表了许多论文:讨论分子大小和布朗运动的《分子大小的新测定》和《热的分子运动论所要求的静止液体中悬浮小粒子的运动》,阐释狭义相对论观点的《论动体的电动力学》和《物体的惯性是否决定其内能》,研究光量子假说的《关于光的产生和转化的一个试探性观点》等。1921年,爱因斯坦成为了不可否认的权威人士。
1919年,世界上“能够理解相对论的两个半人”之一的爱丁顿,通过测量日全食光线弯曲证明了爱因斯坦的预测是正确的。这促使爱因斯坦成为了举世闻名的学术明星和物理权威。有一个这样的传言:爱因斯坦对出版自己作品的出版商说,全世界也许只有十几个人能够理解相对论,但却有几十亿人可以借此明白什么都不是绝对的。
在爱因斯坦的一生中,他都无法理解更不赞成把相对论用在物理学之外的其他领域中,但1905年之后,相对论思想延伸到文学、艺术、哲学、宗教等各个学科中。