





测量火车上两个定点之间的距离的实验让我们明白,光的传播定律和相对性原理相互矛盾 (本章的第七节) 的原因是经典力学中两个不恰当的臆测。这两个臆测分别是:
(1)两件事情的时间间隔 (时间) 和参考物的运动状态没有任何关系。
(2)同一刚体上的两个点之间的空间间隔 (距离) 和参考物的运动状态没有任何关系。
如果我们承认这两个臆测是错误的,那么,本章第七节中的困难就会迎刃而解,因为本章第六节中得出的速度相加定理无法成立。这样一来,光在真空中的传播定律和相对性原理之间的矛盾将会消失,于是便产生了这样的问题:在本章第六节的论述中,既然这两个理论的表面出现了矛盾,那么,我们要如何消除这种矛盾呢?在本章的第六节中,对时间和地点进行论述的时候,参考物既是火车又是铁路路基。如果已经清楚了一件事情相对于铁路路基的地点和时间的情况,那么,如何去确定这件事情相对于火车的地点和时间的情况呢?如果解决了这个问题,是不是就能够化解光在真空中的传播定律和相对性原理之间的矛盾呢?换句话说,我们能够进行这样的假设,任何一件事情相对于一个或者另一个参考物之间的地点和时间之间存在着特定的关系,这种关系促使任意一束光线不管是相对于铁路路基还是相对于火车来说,它的传播速度都是c。这个假设得到了证实,还推导出了一个变换定律,那就是事件的空间—时间值可以从一个参考系变换到另一个参考系中去。
在对这一点进行讨论之前,我们想到一个问题。一直到现在,我们考虑的都是发生在铁路路基上的事情,在数学上,可以把铁路路基看成是一条直线。如同本章第二节所说的,我们可以为这个参考物建立一个由横向和纵向的杆构成的框架,以便把这个框架当作参考物,以此来确定发生在任何一个地方的事件的空间位置。同理,如果火车在无边无际的空间中以速度v在行驶,那么,不管它行驶到什么地方,我们都可以根据以火车为参照物制定的框架来确定火车在空间的具体位置。在这两个框架中,由于固体的不可入性而产生的相互干扰的问题不会造成很大的影响,所以我们可以把这一点忽略不计。
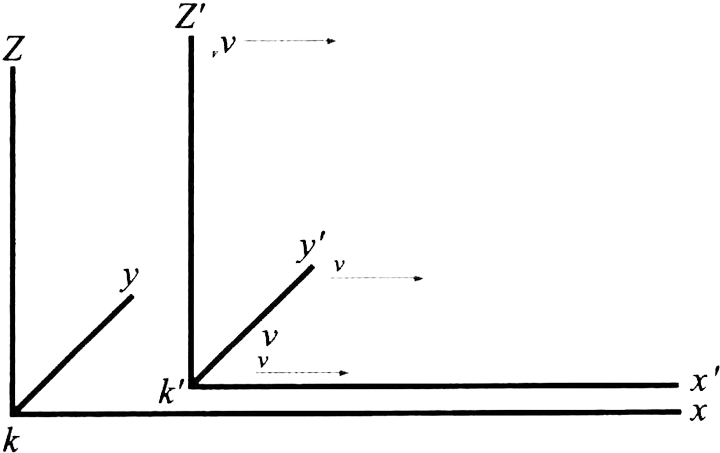
在上面的框架中,我们画出三个相互垂直的平面,命名为“坐标平面” (坐标系) 。这样一来,坐标系 K 对应着铁路路基,坐标系 K' 对应着火车。无论一件事情发生在什么地方,通过坐标平面上的 x 、 y 、 z 三条垂线可以确定它在空间中相对于 K 的位置,而表示时间的t值可以确定它的时间。对于坐标系 K' 来说,可以用与 x 、 y 、 z 、 t 相对应但非相等的值 x' 、 y' 、 z' 、 t' 表示这件事情在空间和时间上的位置。在前面,我们已经详细解释过如何把这些量值当作物理测量结果。
显然,我们可以用公式解决这个问题。如果已经知道了一件事情相对于坐标系 K' 的 x' 、 y' 、 z' 、 t' 的值,那么,这件事情相对于坐标系 K 的 x 、 y 、 z 、 t 的值又是多少呢?在选择关系式的时候,我们一定要明白,不管是对于坐标系 K 还是对于坐标系 K' 而言,同一束光线必须满足光在真空中的传播定律。如果上图表示这两个坐标系在空间中的相对取向,那么,可以通过下面的方程组回答这个问题:
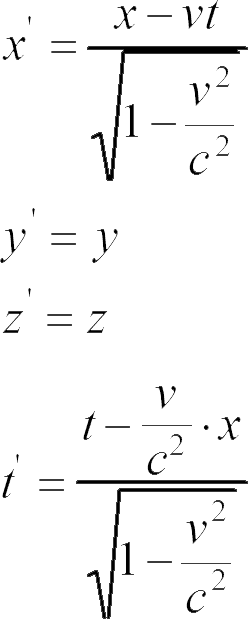
这个方程组叫做“洛伦兹变换”。
如果我们依据的不是光在真空中的传播定律这个假设,而是经典力学中所隐含的时间和长度都具有绝对性这个假设,那么,我们将会得出这样的方程组:
x' = x - vt
y' = y
z' = z
t' = t
这是“伽利略变换”。在洛伦兹变换方程中,如果光速c的值趋于无穷大,就会变为伽利略变换方程。
因此,我们可以发现,根据洛伦兹变换方程可以得知,无论是对于参考物 K 还是对于参考物 K' 来说,都能满足光在真空中的传播定律。例如,如果有一个光信号沿着x轴的正方向发出,所产生的光刺激的前进路线满足下列方程:
x = ct
也就是说,光信号的前进速度是c。根据洛伦兹变换可知,既然 x 和 t 之间有了关系,那么, x' 和 t' 之间必然存在着相应关系,事实的确如此,我们用 ct 去替换洛伦兹变换方程中的第一个方程和第四个方程中的 x 的值,可以得到下面的方程组:
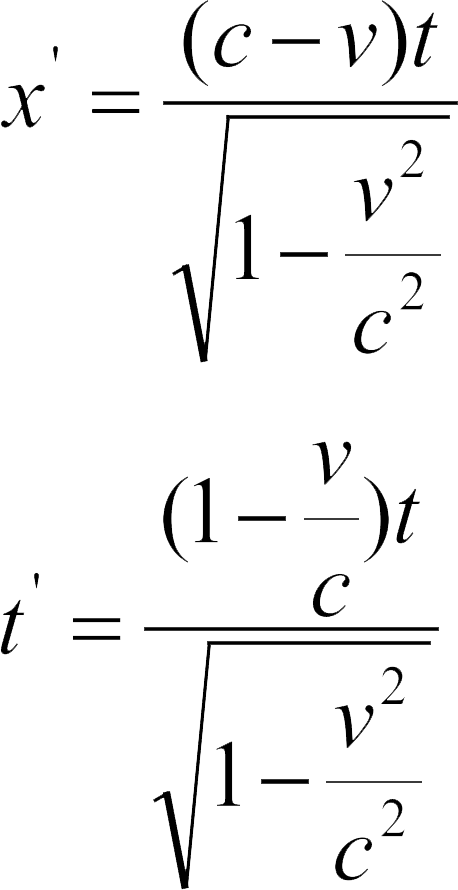
这两个方程相除之后,可以得到下面的式子:
x' = ct'
根据这种解释可以得知,如果参照物是坐标系 K' ,光的传播便会按照这个方程式进行,光的传播速度依然是c。同理,不管光沿着哪个方向传播,我们得到的结果都不会发生变化。当然,这一点并不会让人们觉得惊讶,因为就是根据这个观点推导出来的洛伦兹变换方程。
上文的图表达的是x轴相互重合的两个坐标系的相对取向,我们可以根据图示把问题划分成几个部分,遇到任何一个事件的时候,我们首先去考虑x轴。用横坐标 x 和时间 t 表示坐标系 K' ,用横坐标 x 和时间 t 表示坐标系 K' 。当给出 x 和 t 的值时,我们可以求出 x' 和 t' 的值。
如果一个光信号沿着x轴的正方向前进,可以用方程 x = ct 或者 x - ct =0(1)来表示。
相对于坐标系 K' 来说,光信号的传播速度也是c,所以光信号在坐标系 K' 上的传播可以用方程式 x' - ct' =0(2)来表示。
只要是满足(1)的空间—时间点 (事件) ,一定会满足(2),这个说法显然是正确的。只要
( x' - ct' )= λ ( x - xt ) (3)
成立,那么, λ 一定是常数;因为根据(3)可以得知,当( x - xt )等于零的时候,( x' - xt' )的值一定是零。
如果按照相同的思路考虑沿着x轴的负方向进行传播的光信号,我们可以得到这样的方程式:
( x' + ct' )= μ ( x + ct ) (4)
把方程(3)和方程(4)进行相加 (或者相减) ,然后用 a 和 b 去替代常数 λ 和 μ ,它们之间的关系是:
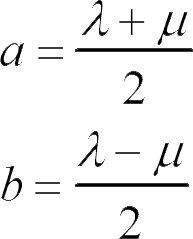
我们得到下面的方程:
|
x'
=
ax
-
bct
x' = act - bx |
(5) |
通过已知的常数 a 和 b ,我们可以求出问题的解。从下面的讨论中确定 a 和 b 的值。
在坐标系 K' 中,原点永远满足 x' =0,把它代入(5)的第一个方程中得到:
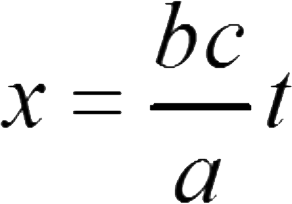
如果坐标系 K' 的原点相对于坐标系 K 的速度是 v ,将会有:
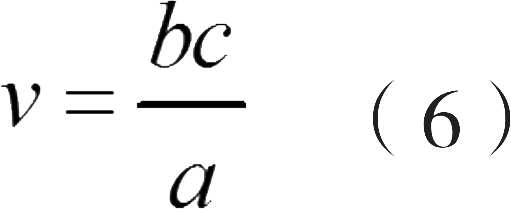
从方程式(5)中可以得出相同的值 v ,如果我们去计算坐标系 K' 的另一个点相对于坐标系 K 或者坐标系 K' 的速度 (指向x轴的负方向) ,那么,速度 v 可以当作两个坐标系的相对速度。
此外,我们由相对性原理得知,通过 K 判断的相对于 K' 处于静止状态的量杆的长度,一定等于通过 K' 判断的相对于 K 保持静止状态的量杆的长度。我们只需要在 K 相对于 K' 的位置上拍张“快照”,就能看到通过 K' 观察到的x轴上的各个点的情况,这需要引入一个特别的t ( K 的时间) 值,如t=0,把t的值代入(5)的第一个方程中得到:
x' = ax
因此,x轴上两个点之间的距离是 x' =1,这是在坐标系 K' 中测量出来的,在我们的“快照”中,这两个点之间的相隔距离是:
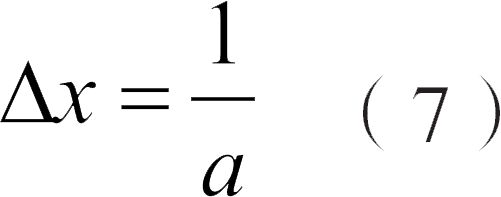
但是,如果我们从 K' ( t' =0)拍摄“快照”,并且用表达式(6)消去方程(5)中的 t ,我们将会得到:
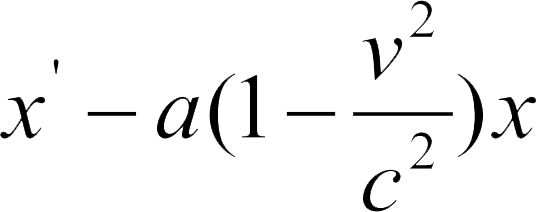
由此可知,如果两个点在x轴上的距离是1 (相对于 K ) ,那么,它们在快照上的距离是:
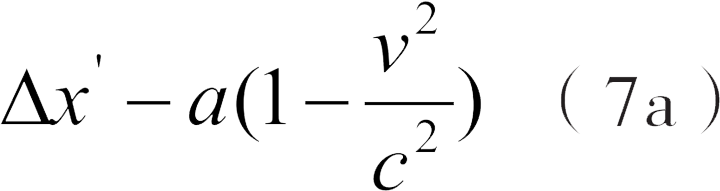
不过,根据上面的描述可以得知,这两个快照一定要相等,所以(7)中的 x 和(7a)中的 x' 相等,这样可以得到:
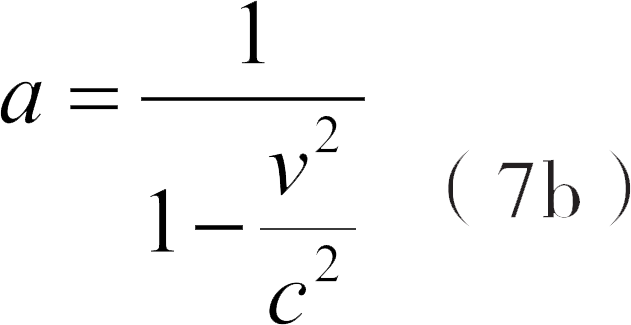
方程(6)和(7b)决定了常数 a 和 b 的值。把这两个常数值代入方程(5)中,我们将会得到前面说过的洛伦兹变换方程中的第一个方程和第四个方程:
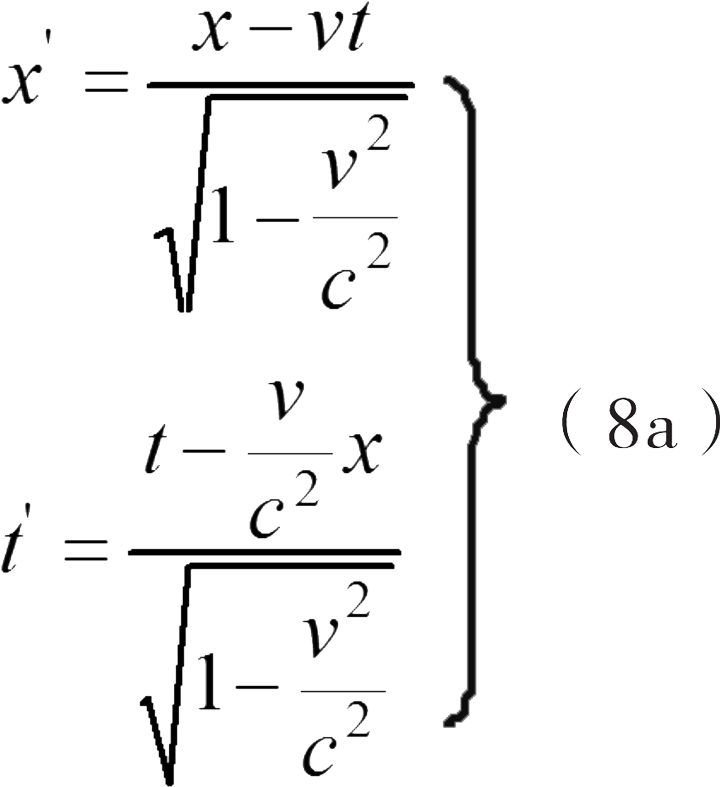
因此,我们获得了x轴上的洛伦兹变换,它需要满足的条件是:
x ' 2 - c 2 t ' 2 = x 2 - c 2 t 2 (8b)
为了了解x轴外面的情况,我们把这个结果进行拓展。在拓展的过程中,只是把方程(8a)保留下来,并且补充两个关系式:
|
y'
=
y
z' = z |
(9) |
这样一来,对于坐标系 K 或者 K' 来说,满足了在它们中的任意方向的光线在真空中的传播速度恒定的公设,可以这样来证明。
假设当时间 t =0的时候,有一个光信号从坐标系 K 的原点发出,这个光信号的传播满足方程式:
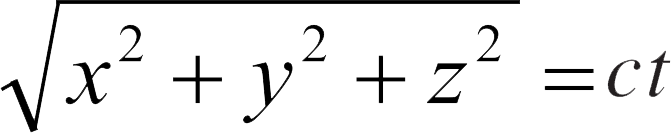
把方程式的两边同时平方,得到:
x 2 + y 2 + z 2 - c 2 t 2 =0 (10a)
通过坐标系 K' 可以得知,光的传播定律和相对性公设要求光信号可以结合在一起,按照公式
r' = ct 或者 x ' 2 + y ' 2 + z ' 2 - c 2 t ' 2 =0 (10b)进行传播。
如果想要从方程(10a)中推导出方程(10b),必须满足方程式:
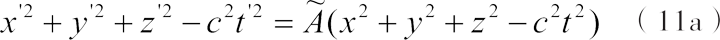
由于方程(8b)要和x轴上的点相互对应,所以
 ,显然,当
,显然,当
 时,由方程(8b)和(9)推导出来的方程(11a)可以满足洛伦兹变换,因此,通过方程(8)和(9)也可以推导出方程(11a)。这样一来,我们就推导出了洛伦兹变换方程。
时,由方程(8b)和(9)推导出来的方程(11a)可以满足洛伦兹变换,因此,通过方程(8)和(9)也可以推导出方程(11a)。这样一来,我们就推导出了洛伦兹变换方程。
当然,我们还要把由方程(8a)和(9)推导出来的洛伦兹变换进行拓展。显然,坐标系 K' 的轴在空间上不一定要与坐标系 K 的轴相互平行。同时,坐标系 K' 相对于坐标系 K 的平移也不一定要沿着x轴的方向。通过仔细思考之后,我们发现借助两种变换可以建立广义的洛伦兹变换,这两种变换指的是狭义的洛伦兹变换和完全的空间变换。完全的空间变换和一个直角坐标系可以由一个指向其他方向的直角坐标系去替换。
通过数学方法可以描述拓展之后的洛伦兹变换的性质:
拓展后的洛伦兹变换指的是用 x 、 y 、 z 、 t 的线性函数表示 x' 、 y' 、 z' 、 t' ,这种性质还要满足关系式:
x ' 2 + y ' 2 + z ' 2 - c 2 t ' 2 = x 2 + y 2 + z 2 - c 2 t 2 (11b)
换句话说,如果把(11b)左边的 x' 、 y' 、 z' 、 t' 替换成 x 、 y 、 z 、 t ,那么,方程(11b)的左右两边一模一样。
洛伦兹变换指的是在狭义相对论中不同惯性系之间的物理事件在空间和时间坐标上相互变换的基本关系式。
假设有 S 和 S' 两个惯性系,它们相对应的笛卡尔坐标相互平行,相对于 S 来说, S' 系沿着 x 轴的方向以速度 v 在运动,当 t = t' =0时,坐标系 S' 的原点和坐标系 S 的原点相互重合,那么,在这两个坐标系中,事件在空间和时间坐标上的洛伦兹变换是 x' = y ( xvt ), y = y' , z = z' , t' = y ( t - vx / c 2 ),方程式中= y (1- v 2 / c 2 )-1/2; c 是光在真空中的传播速度。所有惯性系中的物理定律,一定要保证在洛伦兹变换中形式不变。
在创立相对论之前,洛伦兹的依据是绝对静止的以太观念,在物质运动过程发生收缩得出洛伦兹变换。在洛伦兹理论中,变换过程中引入的量仅仅作为数学上的辅助手段,并没有涉及到相对论的时空观。爱因斯坦的出发点不同于洛伦兹,他在观察到的事实的基础上,借助于相对性原理和光速不变原理两条基本理论,重点去修正运动、时间、空间等基本概念,重新推导出了洛伦兹变换,并且赋予它新的物理内容。在狭义相对论中,最基本的关系式就是洛伦兹变换,狭义相对论中的时空性质和运动学结论,例如同时性的相对性、长度收缩、时间延缓、速度变换公式、相对论多普勒效应等,它们都可以通过洛伦兹变换推导出来。
(1)运动方程属于线性方程。
(2)假设时空具有均匀性和空间具备各向同性。
对于标准位形来说,任意事件在坐标系 S 中的时空坐标( x , y , z , t )及其在坐标系 S' 中的对应坐标( x' , y' , z' , t' ),满足线性变换关系(有些系数还不确定):
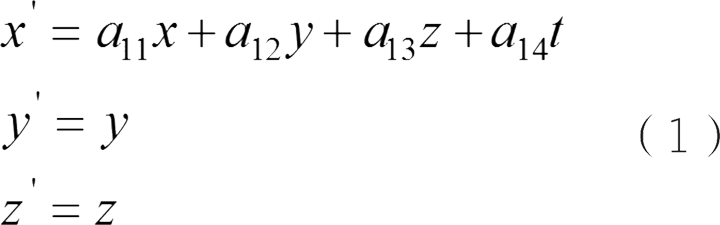
如果 y 和 z 的值是任意的,如果 x = ut ,那么, x' =0,所以
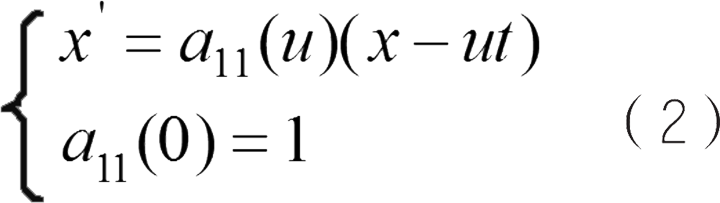
通过相对性原理可知:
x = a 11 (- u )( x' + ut' ) (3)
这说明 t' 是 x 、 x' 的函数:
t' = f ( x , x '( x , t ))= a 44 t + a 41 x (4)
我们可以写出一个方程组:
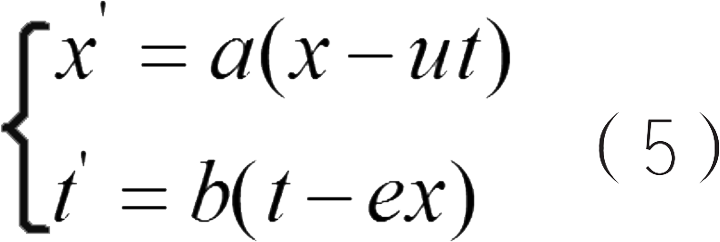
解方程组得到:
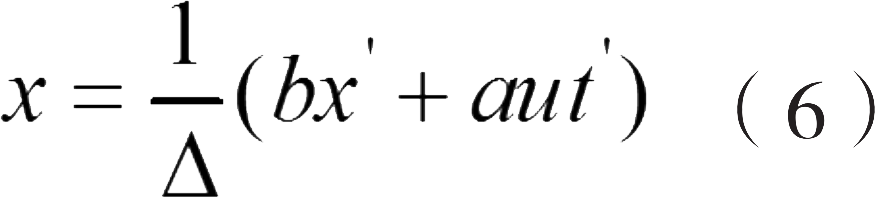
把它和方程式(3)相互结合可以得到 a = b 。到现在为止,我们一直没有使用光速不变原理。假设当 t = t' =0时,有一个球面电磁波离开原点 O 和 O' ,并以速度 c 向前运动,于是有:
x 2 + y 2 + z 2 = c 2 t 2 (7)
x ' 2 + y ' 2 + z ' 2 = c 2 t ' 2 (8)
把方程组(5)代入方程式(8)中,再和方程式(7)联立可以求得:
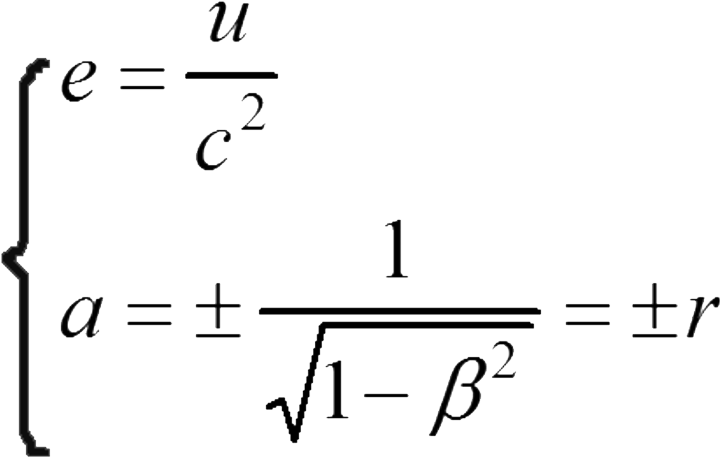
当两个参考系相对静止( u =0)的时候, x = x' ,所以上面的式子是正号。
完整的变换关系是:
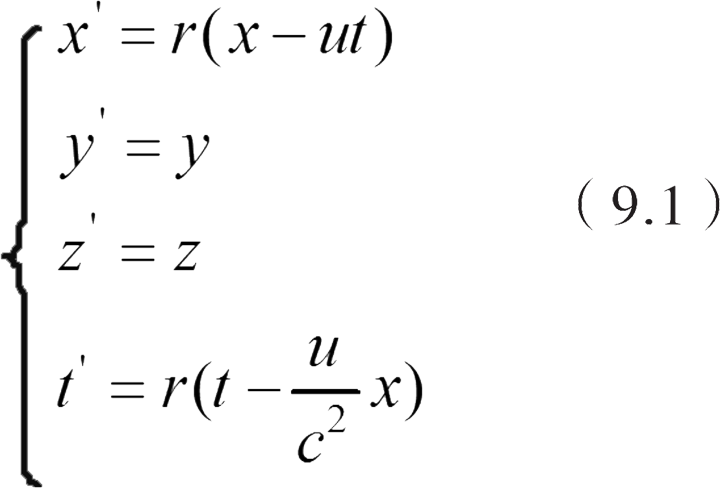
这就是洛伦兹变换。方程组(9.1)还可以用矩阵表示:
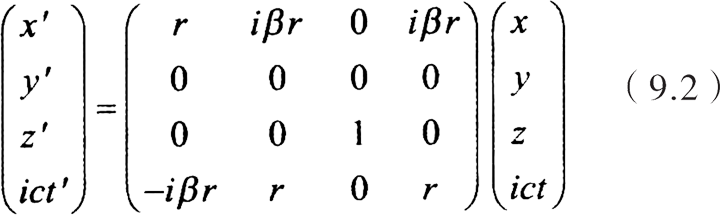
洛伦兹变换的物理本质是:
一、在伽利略变换式 x' = x - ut (或者 x = x' + ut' )的右边乘以系数 γ ,我们就得到了洛伦兹坐标变换式: x' = γ ( x - ut )﹝或者 x = γ ( x' + ut' )﹞。然后让洛伦兹坐标变换式 x' = γ ( x - ut )﹝或者 x = γ ( x' + ut' )﹞的两边同时除以光速 c ,我们就得到了洛伦兹时间变换式: t' = x' / c = γ ( x - ut )/ c = γ ( x / c - ut / c )= γ ( t - ux / c 2 )﹝或者 t = x / c = γ ( x' + ut' )/ c = γ ( x' / c + ut' / c )= γ ( t' + ux' / c 2 )﹞。
二、如果把
t
=
x
/
c
代入
x'
=
γ
(
x
-
ut
)中,可以得到
x'
=
γ
(
x
-
ux
/
c
)=
γx
(
c
-
u
)/
c
,令
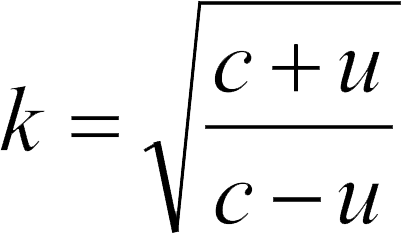 ,可以得到
x'
=
x
/
k
;把
x
=
ct
代入
t'
=
γ
(
t
-
ux
/
c
2
)中,可以得到
t'
=
y
(
t
-
ut
/
c
)=
γ
t
(
c
-
u
)/
c
=
t
/
k
。
,可以得到
x'
=
x
/
k
;把
x
=
ct
代入
t'
=
γ
(
t
-
ux
/
c
2
)中,可以得到
t'
=
y
(
t
-
ut
/
c
)=
γ
t
(
c
-
u
)/
c
=
t
/
k
。
同理,把 t' = x' / c 代入 x = γ ( x' + ut' )中,可以得到 x = y ( x' + ux' / c )= yx' ( c + u )/ c = kx' ;把 x' = ct' 代入 t = γ ( t' + ux' / c 2 )中,可以得到 t = γ ( t' + ut' / c )= γt' ( c + u )/ c = kt' 。
如果光信号到达了 P 点,洛伦兹变换式经过简化后是 x = ct , x' = ct' , x / x' = t / t' = k 。
三、洛伦兹变换式表现出来的是长度膨胀,而不是长度收缩。
在式子 x' = γ ( x - ut )中, x' 指的是通过 s' 系观察 P 点时, P 点和坐标原点 o' 之间的距离。通过 s 系观察时,这个距离( P 点到 o' 的距离)是 L 0 = x - ut ,如果通过 s' 系观察到的距离是 L ,显然, L = γL 0 。这就是长度膨胀。
同理,在式子 x = γ ( x' + ut' )中, x 指的是通过 s 系观察 P 点时, P 点和坐标原点 o 之间的距离。通过 s' 系观察时,这个距离( P 点到 o 的距离)是 L 0 = x' + ut' ,如果通过 s 系观察到的距离是 L ,显然, L= γL 0 。
因此,长度膨胀不是单方面的,而是相互的。
四、在洛伦兹变换式中,不仅体现了长度膨胀,还体现了时间膨胀。我们来分析一下:
把 x = ct 代入式子 t' = γ ( t - ux / c 2 )中,可以得到 t' = γ ( t - ut / c )= γ ( ct - ut )/ c ,然后用 x 去替换 ct 可得 t' = γ ( x - ut )/ c ,式子中的( x - ut )指的是通过 s 系观察到的 o' 点到 P 点的距离,( x - ut )/ c 指的是通过 s 系观察到的光信号从 o' 点传播到 P 点所经历的时间间隔,假设这个时间间隔是Δ t ,那么,通过 s' 系观察到的这个时间间隔是Δ t' = x' / c = t' ,显然,Δ t' = γ Δ t ,这就是时间膨胀。
同理,把 x' = ct' 代入式子 t = γ ( t' + ux' / c 2 )中,可以得到 t = γ ( t' + ut' / c )= γ ( ct' + ut' )/ c ,然后用 x' 去替换 ct' 可得 t = γ ( x' + ut' )/ c ,式子中的( x' + ut' )指的是通过 s' 系观察到的 o 点到 P 点的距离,( x' + ut' )/ c 指的是通过 s' 系观察到的光信号从 o 点传播到 P 点所经历的时间间隔,假设这个时间间隔是Δ t ,那么,通过 s 系观察到的这个时间间隔是Δ t' = x / c = t ,显然,Δ t' = γ Δ t 。
因此,时间膨胀和长度膨胀相同,也是相互的。
五、相对论认为钟慢效应对应着尺缩效应,而我通过观察得知,时间膨胀对应着长度膨胀。由 x / x' = t / t' = k 可以证明这一点。接下来,我们具体解释一下:
假设在 s 系的 x 轴上有一根处于静止状态的刚性棒,棒子的长度是 L 0 ,距离坐标原点比较近的一端是 A 端,另一端是 B 端,有一只蚂蚁从棒子的 A 端向着 B 端爬去,它的速度是 v = u ,相对于 s 系来说, s' 系正沿着 x 轴的正方向运动,运动的速度是 u 。
通过 s 系观察到蚂蚁从A端爬到 B 端所用的时间间隔是Δ t = L 0 / v = L 0 / u 。
通过 s' 系观察到蚂蚁的爬行速度是 v' =( v - u )/[1-( uv / c 2 )],把 v = u 代入式子中,可以得到 v' =0,也就是说,对于 s' 系来说,蚂蚁是静止不动的;而棒子沿着 x' 轴的负方向运动,它的速度是 u ,从 s' 系观察到棒子的 B 端到达蚂蚁的身边所用的时间间隔是Δ t' = L / u 。
1. 如果 L = L 0 / γ ,那么,Δ t =( L 0 / γ )/ u =( L 0 / u )/ γ =Δ t / γ ,Δ t >Δ t' ,这和钟慢效应相冲突。
2. 如果 L = γL 0 ,那么,Δ t' = γ L 0 / u = γ Δ t ,Δ t <Δ t' ,这和钟慢效应相一致。
注意:钟慢效应的特点是我系钟准,彼系钟慢。通过 s' 系观察会得到Δ t <Δ t' 。
总结:在洛伦兹理论中,变换过程中引入的量仅仅作为数学上的辅助手段,并没有物理意义,所以看起来非常繁琐,而且难以记忆。爱因斯坦重新定义了洛伦兹变换,赋予它新的物理内容。通过 x = ct 和 x' = ct' 这两个式子,我们发现洛伦兹变换中包含着长度膨胀和时间膨胀,不用经过推导就可以得知。而且,洛伦兹变换的物理本质就是长度膨胀和时间膨胀。