




统计学发展史简介
此简介并非统计学发展的全貌,也不准备逐一介绍统计史上有关伟人的业绩。在此仅是向初次接触数理统计学的读者简单地就我们身边比较熟悉的事情,片断地说明有史以来到今天为止,统计学是沿着怎样的路径发展而来的,从而让读者有一个初步大概的印象。
一、统计学的起源
Statistics(统计学)一词起源于法语Status(状态)。该词自中世纪以来逐渐演变成含政治意味的State(国家、状态)。因此,统计学原来包含的意义是指对国家的状态进行调查研究。古代的中国和埃及都有过对国家的大事进行统计调查的历史。到了希腊、罗马时代,社会机构日益复杂化,对于从政者来说,掌握国家全面情况的统计知识就变得越来越重要了。亚里士多德所著《国家论》一书中,对很多国家的政治、学问、宗教、艺术和风俗等进行了详细的记述,该书可以认为是后来发展起来的所谓“国势学”的先驱之作。
二、国势学
创立国势学体系的可以说是德国的H.Conring(1606~1681)。他对许多国家的状况进行了记述,并在各大学进行讲演。Conring的国势学和我们现在所说的统计学是明显不同的。他虽然对人口、版图、政体、财政、军备等方面进行了文字性的记述,但几乎不用数字资料。到了18世纪,G.Achenwall(1719~1772)将统计学的性质、意义及范围明确定义为“把国家的显著事项全部记述下来的学科”,并称此学科为Statistik(德文:统计学)。他对Conring的业绩给予了很高的评价,称他为“统计学之父”。不过后人一般都称Achenwall为“统计学之父”。他的主要著作为《近代欧洲各国国势学概论》。Conring和Achenwall都很少做数量方面的观察,没有触及统计资料的实质。十七八世纪,国势学派的学者们常常在各地的大学内进行讲演,因此又被称为“德国大学派统计学”。他们完全不用数量测定值,对图形表格、数字式子十分蔑视,这与英国的政治算术学派是很不相同的。
德国的地理学家Büsching(1724~1793)把统计学看作是地理学的一部分。他收集了各国的资料,并对各国的资料进行了分类比较。丹麦的地理、历史、语言学家Anchersen(1700~1765)将15个国家的状况进行了分类整理,给出了十分容易理解的一览表,他因此被称为“尚表学派之祖”。使用数字、图表的尚祖学派和Achenwall的后继者们之间发生了争论。此后,以Lüder(1760~1819)和Knies(1812~1898)为首的学者对Conring—Achenwall派的统计学进行了激烈的批判。对“统计学作为一门学科其意义到底何在”展开了热烈的讨论。Knies把当时已在英国发展起来的政治算术叫做统计学,认为它是收集、整理和表示资料的科学,即是一种方法论的科学,而把Conring-Achenwall派的统计学叫做国势学。
三、政治算术
17世纪,政治算术学派统计学在英国兴起,这完全是由于当时英国的社会形势影响所产生的结果。1348年、1563年、1592年、1603年和1665年鼠疫流行,伦敦市民对于死亡、出生、结婚、洗礼等含大量数字的报告变得关心起来。1662年,伦敦商人J.Graunt(1620~1674)撰写了《关于伦敦死亡表的观察》一书,成为政治算术学派的鼻祖。他利用寺院提供的有关死亡和洗礼的资料,首先制作了死亡表,并指出某些疾病的死亡人数占全部死亡人数的比例是稳定的。他还发现了不少规律性的现象,例如:男女人数占总人口数的比例大致相等;新生儿中男婴的比例稍高;婴幼儿的死亡率较大;都市的死亡率大于地方的死亡率等等。Graunt给出的各种结论在当时来说显得过于大胆和武断,但是20年后,关于人口方面的事实表明确实存在一些规律性的东西。认识到社会现象中存在规律性,这是Graunt的一个伟大功绩。他所制作的死亡表,直至18世纪末期都还被用于计算人类的死亡率。在法国、荷兰等国,考虑年金(抚恤金、养老金等)时也是以他的死亡表为基础的。
不过,政治算术学派的代表人物一般被认为是英国的经济学家配第(W.Petty,1623~1687)。他是Graunt的朋友,他继承和发展了Graunt的研究工作。根据对人口、土地、财政、经济等各方面的大量观察,配第完成了《政治算术》一书。在书中他第一次用计量和比较的方法,将英国的国力与法、意、荷等国进行了比较研究,目的是要论证英国比其他各国强大。他所感兴趣的是与政治有关的问题,只是从数量方面来处理分析。他提出了一套较为系统的方法,用于对社会经济现象进行数量性的描述和数量性的分析比较,创立了政治算术学派的统计学。这是与排斥数量只讲观念的国势学派的统计学很不相同的。
属政治算术学派的天文学家E.Halley(1656~1742)在配第的全球人口数目估算研究工作的基础上,进一步做了更合理、更精确的人口估算,这是在人口统计方面的极大贡献。特别是他通过对死亡率的研究制作了死亡表,并根据该死亡表对人寿保险年金进行了精确的计算,这是关于人寿保险理论的最早的科学研究。以后各国都仿照Halley的方法进行了这方面的研究,为人寿保险理论打下了基础。遗憾的是,虽然英国后来建立了人寿保险公司,但当时对Halley的计算法似乎不很理解。以Halley的死亡表为根据来计算保险金额的新的保险公司一直到18世纪中期才出现。
英国政治算术学派的影响传播到了整个欧洲大陆,此后涌现了一批(包括在德国的)学者,特别是在人口统计方面提出了一系列以大量观测数据为基础的研究方法。
下面再谈谈数理统计学的基础概率论的发展。
四、概率论的起源与发展
最早涉及原始概率论问题的数学著作的作者名叫L.Pacioli(1445?~1510),他提出了赌博中的一个问题:假设力量不平均的两个竞争者进行比赛,但比赛中途停止,没有最后结果,这时,赌金应该如何分配才合理?这一类问题叫做得分问题(Problem of points)。在那以后的200年间,对得分问题的研究一直没有中断过。在三次方程式的解法上曾引起极大争议的G.Cardano(1501~1576)是精通赌博的,为了防备当时在意大利赌场中流行的欺诈行为,他从数学上下功夫研究了各种赌博的方法,写出了一本《赌博者手册》。
不过概率论的真正历史被认为是从17世纪才开始的。在17世纪中期,B.Pascal(1623~1662)和P.d.Fermat(1601~1665)就赌博中的得分问题经常通信交换意见,用数字方法处理这类问题的研究从此开始了。在当时的赌场中,常用投掷骰子、钱币或翻纸牌的办法进行赌博,有经验的赌博者可能知道某一种情况(事件)出现的可能性大一些或小一些。例如,把骰子连续扔三次,出现面朝上的点数之和为10的次数比9的次数要多些。Pascal和Fermat提出了“概率”这一概念,用来描述某一事件发生的可能性。为了计算有关事件发生的可能次数,又发展了排列组合的理论以及集合论的理论。由此,种种的赌博问题也就迎刃而解了。C. Huygens(1629~1695)所著《骰子赌博的理论》一书,是当时最大的一部力作。
对概率论进行了重要的研究并使之成为数学的一个分支的,是瑞士的大数学家伯努利(J.Bernoulli,1654~1705)。在他所著的四部巨作《推论法》(在他去世后的1713年才出版)一书中,有以他自己的名字命名的法则——“伯努利大数法则”:若在一试验中事件A发生的概率为 p ,将此试验重复进行 n 次,设A发生的次数为 r n ,那么当 n 充分大时
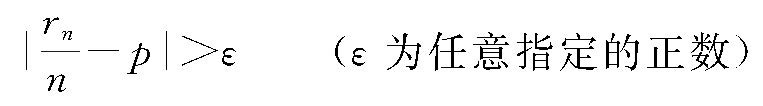
成立的概率可以任意小。例如在投掷骰子时,出现1点的概率
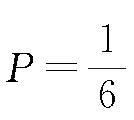 。设投掷n次时1点出现r
n
次,由于有偶然性,
。设投掷n次时1点出现r
n
次,由于有偶然性,
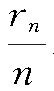 不一定等于
不一定等于
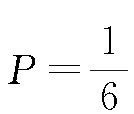 。但是随着n的逐渐增大,
。但是随着n的逐渐增大,
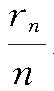 与P的差可以越来越小,也即这个差大于ε的可能性越来越小。比较确切地说,当n趋于无穷大时,
与P的差可以越来越小,也即这个差大于ε的可能性越来越小。比较确切地说,当n趋于无穷大时,
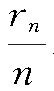 (在统计意义上)趋近于P。这是一个十分重要的法则。
(在统计意义上)趋近于P。这是一个十分重要的法则。
进入18世纪后,de Moivre(1667~1754)所著《偶然论》一书出版,书中有类似于伯努利法则的大数定律,还有更精确的关于概率的数值计算法。
如果上述关于概率问题的研究方法当时能在政治算术上得以利用的话,那么社会统计学的进步可能会早得多、快得多。遗憾的是,在法国出现的概率论和在英国出现的政治算术之间,可以说是什么交流都没有发生过。
此后,在Monmort、Buffon、D.Bernoulli、Bayes、Legendre、Lagrange等研究的基础上,19世纪初,拉普拉斯(Laplace,1749~1827)一举完成了《解析概率论》(1812)这部大作,将概率的定义从有限的情形推广到了连续的情形,并将当时数学界发现的牛顿—莱布尼茨的微积分学应用到了概率的分析理论和计算方法上。虽然拉普拉斯还未给出严格的数学概念,但他很好地应用了高等数学的方法去研究与概率论有关的数学理论,这一点得到了高度的评价。他还将概率论应用于统计学,提出了由部分的调查资料去推断全体的抽样统计法,例如由一部分地区的人口和出生率来估计全国人口数。
18世纪,人们注意到了概率论与自然科学特别是力学、天文学等学科的关系。例如在观测天体运动时会有误差产生,虽经多次测量,由于有误差,得到的总是和真值不同的值,因此产生了如何推断真值的问题。虽然在18世纪,Cotes、Simpson、Legendre、D.Bernoulli等也对此进行了大量的研究,但真正解决问题的是高斯(Gauss,1777~1855)。根据大量的研究和经验,他提出误差值落在(a,b)区间的概率等于该区间上曲线
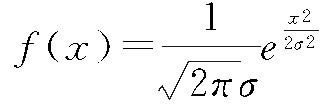 下的面积,这时称误差服从正态分布或高斯分布。正态分布的发现,促使对实测值进行整理分析所用的最小二乘法方面的研究也得以开展,并被应用于实际的统计之中。
下的面积,这时称误差服从正态分布或高斯分布。正态分布的发现,促使对实测值进行整理分析所用的最小二乘法方面的研究也得以开展,并被应用于实际的统计之中。
在以上这些一流数学家的努力下,概率论在理论、应用两方面都得到了很大的发展。
五、19世纪的统计——凯特勒的功绩
19世纪,德国大学派的统计学受到了批判和清算,人们认识到统计学的意义在于它是一门关于统计方法的方法论学科。比利时的凯特勒(A.Quetelet,1796~1874)对此观念的形成产生了很大的影响,他以机械的社会观对社会的各种现象进行数量性的分析,开创了社会统计的一个新纪元。这一时代是所谓统计万能的时代。在1830年以后的20年间,统计学唤起了社会的普遍关心,不少国家有了官方统计,开办了统计学的杂志,成立了各种统计协会等等,同时,国势调查也十分盛行。统计学是由德国大学派和英国政治算术派发展而来的,凯特勒的功绩在于把握住了这两者的本质,在发展政治算术、应用数量观察分析方法的同时,将统计方法应用于社会生活的所有方面,可以说是统计学的新纪元。他学习了数学、物理学、天文学,并将这些知识应用于社会学。他的代表作《社会物理学》“是要给政治科学和精神科学附加上一种以观察和计算为基础的方法,而支配着社会现象的法则和方法则是概率论”。他将道德统计加入到了统计学之中,强调犯罪现象的规律性。他提出了著名的所谓“平均人”的概念,即所有因素都取平均的“典型的”人,有平均的身高、平均的体重、平均的智能、平均的道德观念等。他认为,“平均人”在社会中犹如物体的重心,各个社会成员都围绕着“平均人”摇摆波动。虽然他考虑社会问题的方法有些机械,论点也有不少是过头的,但是随着近代科学的潮流,他的研究却导致了“统计万能”时代的到来。他是第一个将作为数学分支的法国古典概率论引入社会统计研究的学者,因此常被认为是数理统计学的创始人。他对人体测量学也有很大的贡献,他指出人体的测量值是服从正态分布的,因此有时候也把正态分布叫做凯特勒分布。
六、描述性统计学的发展
近代统计学,一方面有和经济学结合以社会复杂的经济问题为研究对象的计量统计学,另一方面还有研究生物现象的生物统计学。对生物统计学做出重大贡献并由此创立了描述性统计学的主要有F.Galton(1822~1911)和K.Pearson(1857~1919)。Galton是创作《物种起源》的达尔文的表弟,出生于知识之家,先在大学学习医学、植物学,后来在剑桥大学热衷于数学研究。他的研究十分广泛,涉及心理学、人类学、生物学、遗传学、指纹学等等,受其表兄《物种起源》大作的刺激,他全力投入到对遗传学的数理统计方法研究之中,终于取得了很大的成绩。他研究了平均值的偏差问题和回归问题,这在统计方法上是一大进步。
Pearson继承和发展了Galton的统计思想。他一生致力于生物测量学、优生学和遗传学的统计方法研究,对一般生物现象进行数量描述,极大地丰富了统计学的概念。他创造了许多统计学用语,例如“频度分布”、“频度分布函数”、“回归”、“相关”、“拟合度”等等。可以说,今天的描述性统计学中大部分内容都是由Pearson整理出来的,大部分统计学用语也是他命名的。他与Galton、Weldon在1901年创办了 Biometrika 杂志。这是一本很有权威的学术杂志,直至今日也是世界上级别最高的统计学杂志之一。他所主办的研究所编制了很多数学用表,为从事统计调查、科学实验以及应用数学等领域的工作者提供了重要的工具。
七、推断统计学的诞生
1920年前后,统计学有了重大的转机,这就是推断统计学的诞生。可以说是由W.S.Gorsset(1876~1937)(笔名叫Student)开始研究,最终由R.A.Fisher(1890~1962)创立而成的。
当时在英国Dublin啤酒公司任技师的Gorsset想要解决啤酒质量的检验问题,可是对所涉及的研究对象(比如啤酒中酵母菌的含量、啤酒对小麦的比收获量等等)却很难获取大样本的数据。他苦心钻研统计理论,终于想出了一种小样本的检验方法——t检验法,并于1906年以“Student”的笔名在 Biometrika 的杂志上发表了。虽然从量上看这是一件很小的工作,但在思想上却可以说是开创了一个新纪元。他的结果后来经Fisher从数学上进行了严格证明,由此诞生了小样本检验的理论。Fisher是很有声望的统计学家、剑桥大学的名教授。起初他在英国Rothamsted试验农场当技师,对农业试验中如何应用数理统计方法的问题进行了深入的研究,导出了分布法则,提出了方差分析法以及各种检验法等。他的巨大贡献在于从统计的意义上明确了推断、检验的含意及其与数学的关系,创立了估计理论和检验理论等统计的理论体系,开拓了统计学的新领域,也就是创立了与过去的描述性统计学所不同的推断统计学。
第二次世界大战以后,推断统计学的研究成为数理统计学的主流,特别是在美国,在理论和应用两方面都有很大的成就。A.Wald是这些研究者中的代表人物之一,《序贯分析》是他的代表作。
八、推断统计学的应用
近代统计学即推断统计学虽然起源于统计方法在农业试验中的应用,但其重要意义远远超出这一范围。在自然科学、管理、工农业生产、社会科学、医学、心理学、行为科学、商业、气象等几乎任何领域,推断统计学都是适用的。以下仅就其在管理部门和社会调查中的应用做一简要的介绍。
首先介绍在批量生产过程中的质量管理。当反复批量生产某种产品时,使用完全相同的原料、完全相同的工具和按照完全相同的生产过程实际上是不可能的,因此无法生产出完全相同的产品。对产品表现出的不均一性,有些原因是可以查明的,对这些影响均一性的因素一定要去掉。不过即使将查明了原因的影响因素全部排除掉,产品之间也还会残存差异。这种差异(变动)被认为是由偶然性(随机性)造成的。对这种偶然性的处置就成了我们统计学的研究对象。也就是说,首先要研究如何查找非偶然性的影响因素,如何制定产品的质量和形状等的规格;其次,要检验实际产品是否符合这些规格,在检验时要用什么样的方法等。以上问题的解决都要用到推断统计学,这样实行的管理就叫做统计质量管理(SQC)。这种管理最早由英国实行,二次世界大战期间,美国通过这种统计质量管理,提高了美国军工产品的质量,给厂家带来了巨额的利润。以后,一些工业发达国家纷纷仿效。20世纪60年代,日本在学习美国统计质量管理的基础上,结合日本的国情,进一步发展完善,发展出全面质量管理(TQC),从而对日本的国民经济发展起到了重要的推动作用。目前,日本的全面质量管理已引起世界上越来越多国家的重视,并在许多国家中得到了应用。我国也在试行全面质量管理。
其次介绍在社会调查中的应用。所谓社会调查,曾被认为是要对全部对象(总体)进行全面调查,从而为将来制订计划和决策准备基础资料。但是,全面调查从时间和经济上来说都是十分困难的。即使只对全面调查数据进行统计处理,等做出决策时总体中的某些因素也可能已经发生了变化。如果我们对总体的某些分布情况有一定的把握,就不必进行全面调查,可以进行部分调查即抽样调查,这从时间和经济上来说都是合算的。根据抽样调查的结果,可以对总体的状况进行估计和推断。由部分推断全部,概率论和数理统计理论起着重要的作用,这是近代统计学的主要特征。关于抽样调查,有很多方法,对此也在进行着大量的研究。实际上,各国在经济统计、国势调查、社会调查、收视率调查、民意测验上等等,采用的几乎都是抽样调查。
部分(抽样)调查的方法不仅在社会统计中应用,也在科学实验中应用,对所有的实验结果也是按部分资料来看待的,故在处理实验资料时要利用统计推断。一般情况下实验数据都不多,因此,要想从中得到一些结论,必须严格按概率论和数理统计理论的有关准则行事。
最后举一个选举预测的例子,从中我们可以体会到正确进行抽样调查的重要性。
美国的盖洛普(Gallup,1901~1984)是新闻学界所熟悉、毕生从事民意调查事业的人物。他在1935年创建了美国民意学会。20世纪30年代,美国的一些报纸杂志也开始纷纷成立专门的机构进行民意测验和选举预测。在1936年美国总统大选的预测中,《文学文摘》( Literary Digest )等杂志社由于预测结果与实际得票率相差太多而被迫停刊,而盖洛普的美国民意学会却由于预测成功而声名大振。《文学文摘》的失败主要是由于抽样的偏差,他们无视一般劳动阶层(上流阶层的人大多数投兰登的选票,而结果却是罗斯福当选);盖洛普却采用配额方法(Quota Method)来抽样,即考虑地区、年龄、性别、支持的党派、收入等种种情况,按一定的比例配额来决定抽样数。实际上,盖洛普的抽样法还不是我们所指的那种随机抽样,他们只是从比例上去控制,而调查员实际上还是根据自己的意愿怎么方便就怎么去调查的,即还是属于一种“有意选择法”,还满足不了随机性的要求。因此,1936年盖洛普预测的成功还只是一种粗糙的结果。
在1948年总统大选的预测中,不但 Crossley 、 Roper 等杂志全部失败,就连盖洛普也失败了。据分析,其原因主要有抽样和访问调查中的问题以及浮动票的预测问题。由于这次失败, Crossley 和 Roper 从此将力量转向市场调查。但盖洛普却对失败进行了认真的反省,根据概率论的原理全面研究了抽样的方法,终于在1950年的中期选举中获得了15年间全国选举预测的最佳结果。此后,盖洛普的名字便成了民意测验的同义词。
九、现代统计学
现代统计学无论是在数学理论还是在应用范围上,都得到了飞速的发展。特别是随着计算机的发展与普及,在应用上开拓了广泛的前景。无论是在自然科学、社会科学还是在医、农、林等各个领域,统计学都已经逐步成为不可缺少的工具。根据作者的理解和体会,现代统计学有以下几个特点:
第一,理论和方法不断完善和深化。
随着实际应用的需要,对数理统计理论和方法提出了越来越高的要求。从线性到非线性、从低维到高维、从显在到潜在、从连续到离散等等,现在基本上都有了相应的较为完备的理论和方法。新的课题和方向也在继续探索研究之中。
第二,计算机及其相应的统计软件已逐步成为统计工作者不可缺少的工具。
大量优秀统计软件的研制成功为统计的应用开拓了新的广阔前景。国外社会科学工作者常用的软件包如SPSS、SAS、DATA-TEST、STATA等等也已逐步引进我国,有些已经被汉化。与此同时,我国的统计工作者也开发研制了各种实用的统计软件。标准统计方法的应用使得计算量再大也变得简易可行,而复杂的、难于从理论上证明的新的统计方法也可以借助计算机模拟进行研究。统计和计算、统计和计算机已经成为不可分割的一体。作为统计学的一个新的分支,计算机统计学(在我国称概率统计计算)正在兴起。
第三,现代统计学正逐步成为一门通用的、研究如何合理有效获取、整理和分析数据的独立的交叉性学科。
我国统计学界在传统上将统计学派分成“社会统计学派”和“数理统计学派”。前者认为统计学是一门社会科学,后者则认为统计学是一门应用数学。我们认为两者都带有一定的片面性。按照目前国际上比较流行的看法,统计学是一门独立的学科,是一种方法论。它的原则既适用于自然科学,也适用于社会科学等诸多领域。因此在某种意义上,可以说现代统计学是一门独立的交叉性学科。
基于这样的认识,在我国统计教育学界两个学派的共同努力下,1998年教育部对原有的本科专业目录进行调整修订时,终于将统计学设置为一级专业学科。而在1998年之前,我国高校本科的统计学专业一直是二级学科(设在经济学学科下的“统计专业”以及设在数学学科下的“概率论与数理统计专业”)。统计学专业的升级,对促进统计学的专业教育,对培养既有数理统计理论基础又有实际应用能力的人才,起到了重要的作用。
可以说,社会科学工作者和数理统计工作者相结合,相互学习,探索社会科学研究领域中的新问题、新方向,无疑是一个可以大有作为的新天地。这也是我们近二十年来在教学和应用实践中的深切体会,在此献给读者,以结束这篇似乎过于冗长的绪言。