




This book is organized as follows.
Chapter2 reviews the development of traffic flow theory from the perspectives of macroscopic,mesoscopic,microscopic and stochastic approaches.Some representative models and methods in literature are summarized and compared.Particularly,various categories of headway/spacing distributions are investigated,such as univariate simple distribution,compositional distribution,mixed distribution and random matrix theory based approaches.The review summarizes four typical approaches in stochastic traffic flow modeling.The literature review forms a solid theoretical background for the book.
As shown in Fig.1.1,we explore the characteristics of empirical traffic flow measurements to reveal the complex,dynamic and stochastic phenomena in Chap.3.We apply the Eulerian and Lagrangian observations to qualitatively and quantitatively study some significant aspects of traffic flow features,including headway/spacing/velocity distributions,disturbances of congested platoons(jam queues)and time-frequency properties of oscillations.This work is the empirical foundation of the stochastic modeling.
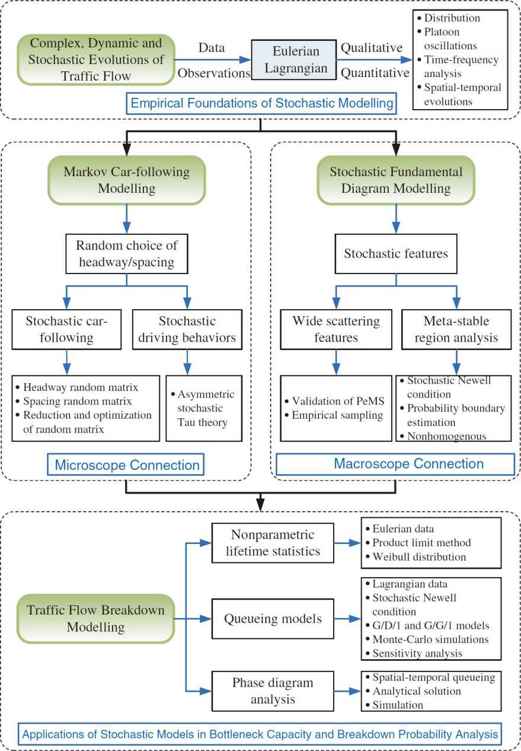
Fig.1.1 Structure of the stochastic traffic flow modeling and applications
In Chap.4,from a microscopic perspective,we link two research directions of road traffic:mesoscopic headway distribution and microscopic vehicle interactions,by proposing a unified Markov state transition car-following model for different driving scenarios(highways and intersections),where random choice behaviors of headway/spacing(unconscious and inaccurate perceptions of time intervals and/or space)are the underlying stochastic sources.The parameters of this model can be directly estimated from NGSIM trajectory data.We also propose an asymmetric stochastic extension of the well-known Tau Theory by assuming that the observed headway distributions come from drivers consistent actions of headway adjusting,the intensity of headway change is proportional to the magnitude of headway on average.
The scattering feature of points on the density-flow plot remains as an attractive topic in the last few decades.In Chap.5,from a macroscopic perspective,we discuss the implicit but tight connection between the microscopic spacing/headway distributions and the macroscopic scattering feature of flow-density plot.Although the scattering feature is influenced by various factors(e.g.,driver heterogeneity and lane-changing/merging behaviors),we believe that may be mainly dominated by the microscopic spacing/headway distributions.Further extending the conventional deterministic reciprocal relations between flow rate and headway,we assume that the reciprocal of average headway of a homogeneous platoon and the corresponding flow rate should follow the same distribution.We examine microscopic driving behaviors that were retrieved from the NGSIM trajectory database.Results show that asymmetric driving behaviors result in a family of velocity-dependent lognormal type spacing/headway distributions.Then,we propose a stochastic platoon model to characterize the distribution of points in spacing-velocity plot.Tests on Performance Measurement System(PeMS)data reveal that the seemingly disorderly scattering points in the macroscopic flow-density plot follow the estimated flow rate distributions when the aggregation time interval is small enough(e.g.,30s).If the aggregation time interval increases(e.g.,to 5min),the measured vehicles probably pass the loop detectors at different velocities and form heterogeneous platoons.It becomes difficult to find a definite distribution model that can fit the distribution of average headway/spacing for various heterogeneous platoons.However,most points in flow-velocity plot still locate within a certain 2D region,whose boundaries can be obtained from homogeneous platoon model.Finally,tests on PeMS verify this boundary property.
In Chap.6,we study the commonly observed traffic flow breakdown phenomena at highway bottlenecks,emphasizing the transition process from perturbations to traffic jams in congested flow.We propose a queueing model to describe traffic breakdown phenomena caused by perturbations of on-ramp vehicles.If this jam queue cannot dissipate before the next vehicle merges into the main road,it often grows into a wide jam and results in traffic breakdown finally.In other words,the traffic breakdown probability directly corresponds with the probability that this jam queue dissipates in a given time period.But different from many previous models that focused on the propagation of jam waves,the proposed queueing theory based model emphasizes the size evolution of a jam queue(local congested vehicle cluster)instead of its spatial evolutions.We discuss the close relationship between TF-BP and the jam wave propagation phenomena with concentration on the evolution of jam queue size.Furthermore,a simplified queuing models are proposed based on Newells simplified car-following model,where the formation and dissipation of jam queues are treated as comprehensive effects of stochastic joining and leaving processes for upstream and downstream vehicles,respectively.Test results show that the simulated breakdown probability curve fits well with the empirically observed Weibull distribution type breakdown probabilities.This agreement indicates that this new model captures the stochastic nature of traffic flow dynamics and therefore accounts for the probability of breakdown phenomena.Finally,we analytically derive the phase diagram that is useful for presenting the evolution process for different traffic flow phases and quantitatively determining the phase transition conditions.
Chapter7 summarizes this book and recommends a few future research directions.