下载掌阅APP，畅读海量书库
立即打开
• Negative exponential distribution
Let h denote the random variable of headway．Negative exponential distribution describes the interarrival time as Poisson process．Events occur continuously and independently at a constant average rate．It is appropriate when traffic flow rate and density are small．
The PDF is
where λ is the rate parameter．It indicates aggressive driving behaviors when λ is relatively large，while it indicates timid driving behaviors when λ is relatively small．
The CDF is
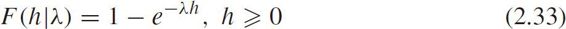
The expectation and variance of headway are
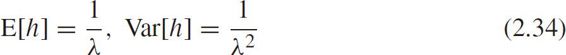
Define the maximum likelihood function as
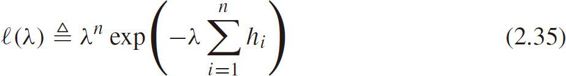
Let
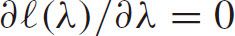，we have the following maximum likelihood estimator（MLE）
where
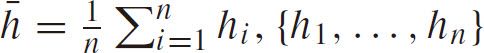are samples．
• Shifted exponential distribution
Since the probability of headway near zero is large in negative exponential distribution，to avoid the extremely short headways，the PDF is shifted rightwards with a deterministic positive value．
The PDF is
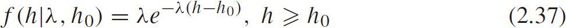
where h 0 is the translation parameter．
The CDF is
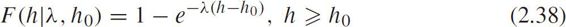
The expectation and variance of headway are
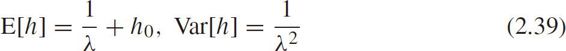
Define the maximum likelihood function as
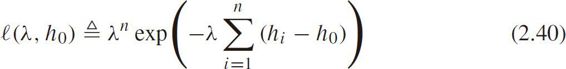
Let
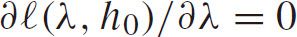，we have the MLEs
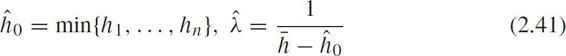
• Gamma distribution（Pearson type III distribution）
Gamma distribution is a two-parameter family of continuous probability distributions used to model headway commonly．
The PDF is
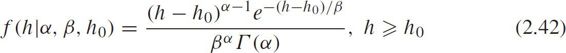
where
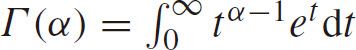is the gamma function with a shape parameter
α
and a scale parameter
β
．
The CDF is
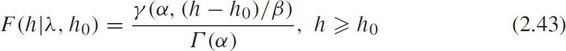
where
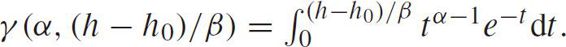
The expectation and variance are
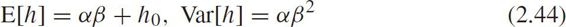
There is no closed-form solution for α and β ．They can be numerically approximated by using Newton's method，method of moments，etc．However，Gamma distribution cannot be suitable to depict headway distribution when the shape parameter is larger than 1 because the bell-like shape gives low probability to short headways．
• Shifted lognormal distribution
If log（
h
−
h
0
）follows the normal distribution
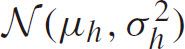，then
h
belongs to shifted lognormal distribution．The lognormal relation holds if the change in a headway during a small time interval is a random proportion of the headway at the start of the interval，and the mean and the variance of the headway remain constant over time（Luttinen 1996）．Shifted lognormal distribution is widely used in headway/spacing modeling in both scenarios of continuous and interrupted transportation facilities．It is also closely related to car-following models as well．
The PDF is
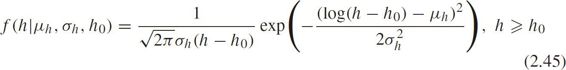
where μh ， σh are the mean and standard deviation，respectively，of the headway's natural logarithm
The CDF is
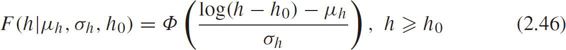
where Φ （•）is the standard normal distribution function．
The expectation and variance of headway are
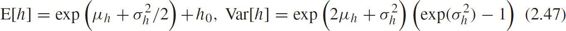
Define the maximum likelihood function as
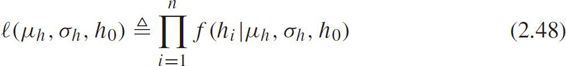
Let
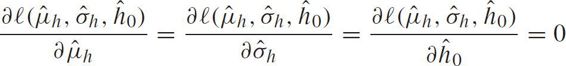
we have the following MLEs
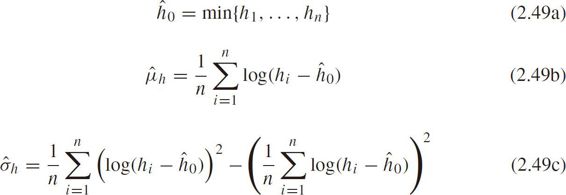
The simple univariable distributions are incapable of describing both sharp peak and long tail properties of headway/spacing．Because of the coexistence of two main traffic flow states，i.e.，free-flow headways and car-following headways，whose distributions are significantly different．So it's better to incorporate the compositional distribution functions.
The compositional PDF of headway is defined as f （ h ），i.e.，
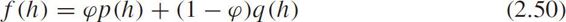
where0≤ ϕ ＜1 is the proportion of constrained headways in car-following states， p （ h ）is the PDF of constrained headways， q （ h ）is the PDF of free-flow headways.
According to the convolution formula，we have
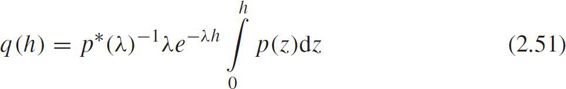
where p * （ λ ）is the Laplace transform of p （ h ），i.e.
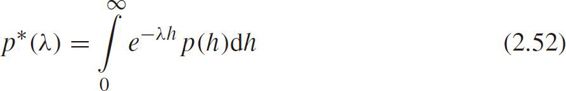
• Hyperexponential distribution
Schuhl（1955）first applied Hyperexponential distribution to model headway，known as Schuhl's（composite exponential）distribution.
The PDFs are
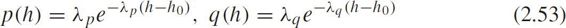
where λ p ， λ q are parameters of exponential distributions for car-following and free-flow states，respectively.
• Hyperlang distribution
Dawson and Chimini（1968）suggested the Erlang-distribution as a model for car-following headways，i.e.，
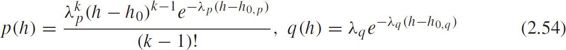
where
，
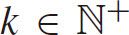λ
p
，
λ
q
are parameters of car-following and free-flow distributions，respectively．
h
0
，
p
，
h
0，
q
are the translation parameters．Luttinen（1996）pointed out that the hyperlang distribution has an exponential tail，and the shape of the PDF is similar to empirical headway distributions.
It is found that many stationary distribution models could fit the empirical data of free flow but not congested flow．One way to solve this problem is to use the mixed headway distribution models．For example，in the M3 model（Cowan 1975），the headways of free-driving vehicles and those leader-following vehicles were assumed to follow different PDFs．But the calibration of mixed models is usually tedious，if we want to fit the empirical distributions with a high accuracy.
• Semi-Poisson distributions
Buckley（1968）proposed the semi-Poisson model that described the fluctuations in car-following states，conjectured there was a zone of emptiness in front of each vehicle，and compared it with Gamma distribution，shifted Gamma distribution，exponential distribution by using field measurements．Wasielewski（1974）applied non-parametric method to calculate constrained headway in semi-Poisson distribution.
The PDF of semi-Poisson distribution is
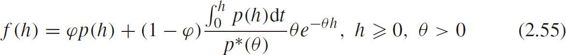
where
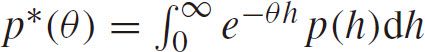is the Laplace transform of
p
（
h
）.
Semi-Poisson distribution defines two common headway distributions for car-following scenarios，i.e.，
Gamma distribution and its Laplace transform
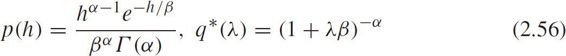
Gaussian distribution and its Laplace transform
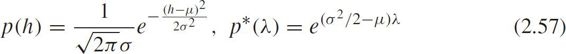
where μ and σ are the expectation and standard deviation of Gaussian distribution.
Branston（1976）proposed a mixed model of a generalized queuing model and semi-Poisson model．The PDF for free-flow headway is
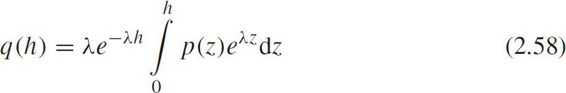
where 1/ λ is the average headway．Assume headway follows lognormal distribution in car-following mode as
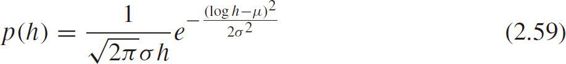
then the PDF for mixed headway is
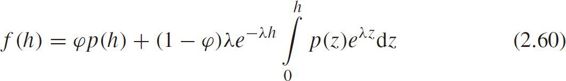
Krbálex and Sěba（2001）showed that traffic data from different sources belonged to a class of random matrix distributions．Abul-Magd（2006）applied the random matrix theory（RMT）to the car-parking problem and adopted a Coulomb gas model that associated coordinates of gas particles with the eigenvalues of a random matrix，in which the Wigner surmise for Gaussian unitary ensemble（GUE）was given by
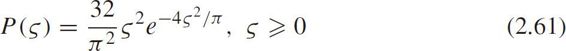
where ς is the space gap，i.e．spacing minus vehicle length.
Abul-Magd（2007）pointed out that RMT modeled the Hamiltonians of chaotic systems as members of an ensemble of random matrices that depended only on the symmetry properties of the system and GUE modeled systems violating time reversal symmetry．In the phase transition from the free-flow state to the congested state，the GUE of RMT is
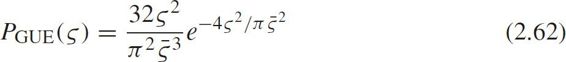
where
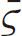is the mean space gap.
Space gaps in free-flow traffic are uncorrelated and follow the Poisson distribution
More recently，models based on headway/spacing distributions and state transitions received more interests．For example，Jin et al.（2009）revealed that the distributions of departure headways at each position in a queue approximately followed a certain lognormal distribution except the first one by using video data collected from four intersections in Beijing．Wang et al.（2009a）estimated a cellular automation model for spacing distribution.
