




土壤溶质迁移流失过程应该是一个降雨-径流-溶质流失的过程,实质上也就是降雨-径流过程导致对流、扩散、土壤侵蚀和伯努利效应相互作用的过程。我们希望通过室内模拟试验,深入了解土壤溶质迁移机理及其过程,量化每一个途径导致溶质迁移的贡献率,揭示其内在机理。国内外学者已进行了大量的试验研究与理论分析,并提出大量的降雨-径流溶质迁移模拟模型,但均未量化各种迁移途径。
1974年,Kuo和Lotse [57] 根据试验研究结果发现了一个简单的幂函数形式的动力学方程,该方程可以模拟土壤中磷随着时间变化的分解、吸附、转化过程;1974年Bauley等 [58] 提出养分传输的概念模型;1975年,Bruce等 [59] 提出土壤养分传输模型; 1975年,Frere等提出农业土壤溶质迁移模型(agricultural chemical transport model, ACTMO),1980年又建立了改进型溶质-径流-侵蚀-农业管理模型(chemicals, runoff, and erosion from agricultural management systems,CREAMS) [60 ~ 61] ;1979年Barrow [62] 、1980年Chien和Clayton等 [63] 利用幂函数为框架对模型进行修正,取得了较好的模拟效果。Sharpley等 [51] 通过室内一定水土比振荡试验模拟,研究磷的分解、吸附、转化过程。总结前人的研究结果,Ahuja [64] 认为与室内振荡试验过程相似,在降雨-径流-表层土壤溶质相互作用的过程中模拟了土壤养分在径流中的扩散和传输;1984年,Haith等 [65 , 66] 提出康奈尔养分模拟模型(cornell nutrient simulation, CNS);1988年,Wallach [67] 等也在总结前人研究成果的基础上,提出了土壤溶液养分向地表径流传输扩散的模型。这些模型均能很好地反映土壤养分水蚀流失,但由于这些模型仅考虑了土壤表层某一薄层养分与降雨和径流的相互作用,并没有涉及土壤、作物等其他因子的影响,因而在理论上有不足之处,数学基础也不够严密。Ahuja等进行了室内人工模拟降雨试验,其结果表明土壤溶质浓度与降雨强度、坡长、坡度及土壤表面植被情况有着密切关系。1994年,Steenhuis等 [68] 得出一个简单的预测土壤渗流出的溶质浓度的方程。2004年,Vadas等 [69] 通过对地表土壤施加粪肥(牛粪、家禽粪和猪粪)来研究地表径流磷分解、吸附与迁移,并在模型基础上建立了适合各类粪肥径流磷迁移模型。
1975年,美国农业部农业研究组织 [60] 根据流域侵蚀和养分流失特征,建立了ACTMO模型。1977年,Donigian [19] 模拟径流传递过程,建立了非点源污染模型(non-point pollution system, NPS)。在NPS模型的基础上,Donigian [20] 对其进行修正,建立了适合农业土壤养分径流流失的模型(agricultural run off management, ARM),该模型不仅能从侵蚀角度模拟降雨侵蚀过程,而且能模拟养分在径流作用下迁移、扩散、释放的过程。Young等 [25 ~ 27] 于1985年和1987年以流域为研究单元建立模型(agricultural non-point pollution, AGNPS),该模型主要用于研究和预测次降雨过程中径流流量、侵蚀传递的泥沙、径流液中有效N和P的浓度、泥沙中N和P的含量。此外,还有1971年和1979年的NONPT模型 [70 , 71] 、1980年的PRM模型 [72] 、1980年的SPNM模型 [72] 、1981年的SWMM模型 [73] 、1982年的ASWM模型 [74] 、1986年的CPM模型 [75] 、1989年的PLIERS模型 [76] 、1998年的EUROSEM模型 [77] 等,这些模型从土壤侵蚀、土壤养分流失、土壤水分平衡等方面系统地研究了坡面或流域单元内养分的流失过程及机理。
在绝大部分土壤溶质迁移规律中,土壤溶质的基本迁移机制有3种:对流、扩散和水动力扩散。将土壤溶质迁移的3种机理与连续流方程相结合,可形成土壤溶质迁移的对流扩散方程(convection-diffusion equation, CDE) [78 , 79] 。
1989年,Wallach等 [80] 的研究结果表明,坡地土壤溶质的迁移过程主要有两个过程:第一个是通过扩散作用使得土壤溶质迁移到地表径流,即动力扩散过程;第二个是土壤溶质溶解于地表径流并流出土壤进入地表水,即溶解迁出过程。这两个过程并不是独立存在的,而是相互制约的,所以可将二者统一为一个系统的土壤溶质的迁移过程,只不过是侧重点在动力扩散过程。研究结果证明了当降雨强度不大时,坡度和坡长的大小都会影响土壤溶质迁移至径流的过程。2009年,王全九等 [81] 的试验结果表明,表面上是坡度影响土壤溶质迁移,实质上是通过坡面径流流量和流速来实现的,径流流量起着主导地位,并可用幂函数来描述田间坡面土壤溶质的迁移过程。
郭太龙和王全九 [82] 通过对比分析坡面水流的水动力参数与径流溶质迁移量之间的关系,研究了不同地表状况下黄土坡面土壤溶质随径流迁移的水动力学特性,以求深入了解和认识坡面土壤侵蚀中溶质随径流迁移的本质机理。他们认为,通常情况下坡面水流的水深都很小,仅为几毫米或更小,则可近似认为水力半径等于平均水深,故可写为

式中,n为通常糙率系数;
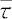 为水流的平均剪切力,N/m
2
;γ为水的容重,N/m
3
;J
0
为坡面水流的能坡,由于坡面的坡度较小,可近似认为J
0
≈sinθ,θ为坡面角度;h为水头高度,m。
为水流的平均剪切力,N/m
2
;γ为水的容重,N/m
3
;J
0
为坡面水流的能坡,由于坡面的坡度较小,可近似认为J
0
≈sinθ,θ为坡面角度;h为水头高度,m。
在土壤溶质均衡模型中,考虑土壤中溶质的输入与输出等量关系和土壤溶质的变化关系,描述土壤溶质的状况,并得出运动用水量平衡方程。根据质量守恒原理,水分输入与输出之差等于所研究土体水分储量的变化。可用式(1-2)来描述一定时段内的土壤水量平衡
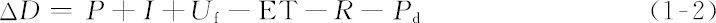
式中,ΔD为所研究土体内土壤水储量的变化,mm;P为计算时间段内的降雨量,mm;I为计算时段内的有效灌水量,mm;U f 为计算时间段内的深层水上升补给量,mm;ET为计算时间内作物蒸散量,mm;R为计算时间内土壤地表径流流量,mm;P d 为计算时间内土壤深层排水量或者渗透量,mm。
在现实土壤中不仅存在着大小不同的孔隙,而且土壤溶质和壤中流在一部分孔隙中运动迅速,在另一部分孔隙中于试验时间内基本不动。为此,对对流扩散方程进行了修正,提出了可动水体与不可动水体的概念,同时认为溶质在迁移的过程中,可动水体与不可动水体之间还存在着物质交换。Coats和Smith [83] 首先提出了稳态条件下包括可动水体与不可动水体的两区模型。随后,van Genuchten等 [84] 用两区模型研究了溶质在土柱中的运动。Chen和Wagenet [85] 提出了里管流模型。Gerke和van Genuchten [86] 提出了优先流双孔隙体系的两区模型。
坡面水沙迁移包括土壤侵蚀流失和地表水汇流两个方面,均是世界范围的环境问题。严重的水土流失不仅会破坏土地资源,淤塞江河引起洪水灾害,而且还会污染水质,破坏水资源。降雨引发的山洪、泥石流、滑坡等水体汇流灾害成为雨季仅次于大洪水的自然灾害。特别是在暴雨或大暴雨的条件下,土壤极易遭受侵蚀,表层水土流失严重,特殊地区会出现滑坡和泥石流等剧烈的水土流失现象。目前,国内外的研究学者们从多方面去研究水土流失问题,尤其是土壤侵蚀形成的物理基础和坡面产流的形成机理,现就国内外在水土迁移方面的研究做简单介绍。
随着研究学者对土壤侵蚀认识的积累,建立了许多事件、概念、机理性等模型。土壤侵蚀模型的研究史中,Meyer等 [87] 开发研制的USLE模型是土壤侵蚀研究史上的一个里程碑。1978年,Wischmeier和Smith [88] 提出了著名的通用土壤流失方程(universal soil loss equation, USLE);1997年,Renard等 [89] 进一步得到经验土壤侵蚀预报模型(revised universal soil loss equation, RUSLE)。2004年,江忠善和郑粉莉 [90] 在通用土壤流失方程的基础上,针对黄土高原坡陡和浅沟侵蚀严重的特点,提出了包括浅沟在内的土壤侵蚀预报模型的基本结构形式,为研究浅沟侵蚀及其预报提供了重要的思路。为了进一步改进土壤侵蚀的预报和控制方法,新的土壤侵蚀预报物理模型被开发出来,如CREAMS模型 [91] 的侵蚀和沉积子模型;SEDD模型 [92] 和AnnGNPS模型 [93] 都是事件模型,用于模拟农业流域中的径流、泥沙和营养输移;WEPP模型是由美国农业部协同其他一些机构进行研制和开发 [94] 的,是基于侵蚀发生过程的土壤流失量预报模型。刘宝元等 [95 , 96] 、史婉丽等 [97] 对WEPP模型的应用范围和条件进行了评价;雷廷武等 [98] 对WEPP模型中细沟侵蚀模型的正确性进行了分析和验证;缪驰远等 [99] 把RUSLE和WEPP模型运用于四川遂宁径流小区,但模拟结果不理想。Beasley等 [100] 研究的ANSWERS模型认为径流和侵蚀过程互为影响,但没有列出细沟侵蚀,且忽略了沟道侵蚀。1998年,Morgan等 [101 , 102] 研究的EUROSEM模型是一个预报地块和小流域水蚀的事件动态模型,能模拟坡面细沟和细沟间的泥沙传输、侵蚀与沉积过程,能提供径流、泥沙、暴雨水文过程图和暴雨泥沙过程图。1981年Smith [103] 和1990年Woolhiser等 [104] 研究的KINEROS模型,认为泥沙输移是在由沟道、河、湖、库等元素组成的网络共同作用下完成的,雨滴溅蚀与降雨量的平方成正比,径流侵蚀可根据泥沙传输能力的盈余计算得到,坡面侵蚀不分细沟和细沟间侵蚀,沟蚀不考虑雨滴溅蚀。1988年,Lopes和Lane [105] 研究的WESP是一个事件模型,土壤侵蚀与土壤表面的平均剪切力呈正比关系,当水流剪切力大于临界剪切力时,就会发生沟道侵蚀,基于WESP模型的次降雨泥沙预报并不理想,但总泥沙量预报与结果吻合较好,土壤的最初含水量影响径流和泥沙。
随着土壤侵蚀模型研究的发展,土壤侵蚀过程的机理研究被进一步细化,主要研究方向分为雨滴溅蚀、细沟侵蚀和地表薄层漫流剥蚀。
雨滴击溅是降雨侵蚀的首要环节。降雨不但通过击溅作用于地表土壤而做功,导致土粒分散、溅起和输移,而且通过打击坡面径流,影响坡面径流运动。Hudson [106] 通过纱网覆盖的方法研究了雨滴击溅对坡面土壤侵蚀的影响,得出在雨滴击溅的作用下,通过给裸地坡面覆盖沙网在一年内可以使每英亩(4047m 2 )土地的水土流失减少96.69%。吴普特等 [107 , 108] 通过改变雨滴降落高度的方法研究雨滴击溅作用对坡面薄层水流输沙的影响,得出雨滴的侵蚀量一般占总侵蚀量的70%以上,坡面所产生的泥沙绝大部分由雨滴击溅所致。Zhang等 [109] 和Gabet等 [110] 研究了雨滴击溅对坡面输沙的影响,发现坡面薄层水流与溅蚀关系明显,对侵蚀产沙有较大制约作用。李光录等 [111] 采用2种坡度、2种雨强和1~6mm不等的6组不同径流深度研究有无雨滴打击土壤表面时薄层水流对土壤流失量的影响,得出雨滴击溅作用对薄层水流的扰动系数随水流深度的增大呈线性减小趋势,结果表明雨滴击溅作用是薄层水流泥沙剥蚀的主要动力。Tognacca等 [112] 和Gregoretti [113] 的研究表明,在径流作用下,导致沟道中松散物质起动的主要因素是径流剥蚀作用导致的外力,而不是由于物质内部的原因引起。雨滴打击能够使坡面薄层水流由层流变为紊流或扰动层流,从而增加其侵蚀能力。雨滴击溅试验结果显示,随薄层水流深度的增加,泥沙剥蚀量减小 [114 ~ 117] 。王光谦和李铁键 [118] 指出,雨滴击溅与径流侵蚀冲刷是坡面薄层水流侵蚀不可分割的两个方面。王光谦和胡春宏 [119] 指出,坡面土壤侵蚀的过程是一个连续的、发展的变化过程,侵蚀方式和侵蚀形态会随着时间的变化而发生变化,因此对坡面径流流态的研究要考虑其时空变化规律。韩浩 [120] 指出,在降雨条件下坡面径流泥沙起动研究中考虑雨滴侵蚀力的作用是合理的。2009年,Wei等 [121] 通过建立60~180mm/h区间内5组不同降雨强度来模拟土壤侵蚀,建立了水土流失预测模型。
该项试验研究在20世纪30年代初始于美国,苏联较其晚16年,中国晚20年。最早进行的模拟降雨试验是从降雨量方面进行模拟的。1932年,美国Duley和Hays [122] 开展的侵蚀试验小区面积为1.5m×0.85m。Zingg [123] 于1940年在2.44m×1.22m的试验小区上利用人工降雨研究坡度对土壤侵蚀量的影响。20世纪40年代,Laws和Parsons [124] 研究了雨滴的大小、滴谱、雨滴终速以及它们与降雨强度的关系,为人工模拟降雨提供了重要的依据。Woodburn [125] 于1948年在人工降雨的条件下进行了雨滴溅蚀量与降雨持续时间的定量研究。他把试验土样盛在一个小容器内,让其受雨滴击溅一定时间,称出降雨前后试验土样的干重,用两者之差作为土壤溅蚀量。1945年,Ellison [126] 利用人工模拟降雨进行了降雨强度和雨滴下降速度对土壤溅蚀量的试验,并观测了雨滴在不同大小和速度下溅散泥沙颗粒的距离。1969年,Meyer和Wischemeier [127] 在试验室通过人工降雨,用玻璃球作为无黏性床沙质进行了径流冲刷的模拟试验,从而认识到坡面流期间,土壤表面细沟的出现受坡度、流量和降雨的影响;侵蚀强度随坡度和流量的增大而增大;降雨的作用是使表面平坦,从而使细沟化的粗糙表面变得光滑。1975年,Foster等 [128] 在室内用人工模拟降雨研究了坡面径流在凹形坡地上的输沙过程。1981年,李鲁明等 [129] 利用模拟降雨在一个4.572m×1.524m×1.219m的可自由调节坡度的水槽内通过填充中值粒径为0.35mm的土粒的方法,进行了地表径流引起的土壤侵蚀试验。
为了有针对性地研究溶质迁移规律,从解释坡面溶质迁移临界现象的角度来探讨临界因子对溶质迁移的影响较为简便直接。临界现象是指临界点附近发生的现象,坡面水沙迁移临界现象是指水沙迁移量随着影响因子数值的增加而突然下降或突然上升的现象。专家、学者们观察到的水沙临界现象有很多,如降雨强度不变时,随着地表径流流量的增加,溶质迁移量先增加再突然骤降再增加;溶质迁移量随着地表坡度的增加,先增加再降低,等等。归纳起来,造成溶质迁移临界现象发生的主要影响因子为临界降雨-径流因子、临界土壤因子和临界地形因子。
降雨和径流是土壤侵蚀的动力来源,降雨对坡面的作用主要体现在雨滴的打击,径流则是直接冲刷坡面并搬运泥沙。坡面土壤侵蚀的过程是一个连续的、发展的变化过程,侵蚀方式和侵蚀形态会随着时间的变化而发生变化,因此对坡面径流流态的研究要考虑其时空变化规律。坡面水蚀的主要侵蚀动力来自降雨及其产生的地表径流,径流流量的大小与降雨强度及降雨量紧密相关。李光录等 [111] 指出,降雨对土壤侵蚀的影响主要体现在降雨强度、降雨量等方面。Foster等 [128] 认为存在着发生细沟侵蚀的临界流量。Savat等 [130] 的试验表明,当坡面径流佛罗德数(Fr)为2~3时,细沟发生的概率很大。Rauws等 [131] 基于试验数据,认为3~3.5cm/s的剪切流速是细沟发生的临界值。蔡强国和王平贵 [132] 通过回归分析发现,细沟发生的临界水流动力与土壤抗剪强度呈线性增加关系。1992年,陆兆熊和Merz [133] 的试验结果表明,坡面细沟侵蚀的临界剪切地表径流流速为7~8cm/s。张科利等 [134] 研究了细沟侵蚀发生临界水流的条件,认为Fr>1是细沟发生的临界水动力条件,为细沟发生的判断提供了基础,但研究中未涉及降雨因素对细沟侵蚀的影响。雷阿林 [135] 提出用雷诺数、佛罗德数和过水断面单位能量为判断不同侵蚀方式出现的水动力学指标,并运用试验方法确定出细沟侵蚀的动力临界条件。
降雨和径流在坡面水沙迁移过程中的作用不可忽视,现有对临界降雨-径流因子的研究多侧重于细沟侵蚀,对漫流和基流过程中水沙迁移过程的研究很少;同时,临界降雨条件和临界径流条件之间的关系如何转换,转化机理是什么,又应分别采用怎样的指标来表征两者的临界状态等方面的研究也都很少。2010年和2011年,李君兰等 [136 , 137] 对水沙迁移临界条件的研究成果大多是针对细沟侵蚀这一特例现象进行的,尚缺乏对水沙迁移过程中地表漫流剥蚀和细沟侵蚀同时存在条件下土壤流失量及地表径流流量的临界现象的研究。
临界土壤因子包括土壤抗剪切力、土壤特性、土壤初始含水量、土壤表面水分供给情况、地表覆盖类型、温度等。其中土壤特性还包括土壤颗粒密度、容重、孔隙率、土壤含水量、饱和度、渗透系数、土壤水分压力等。土壤对降雨-径流击打冲刷的抵抗作用主要分为抗蚀性和抗冲性两种性能。土壤的临界抗剪切力是定量分析坡面水土流失过程的一个重要指标。Gilley等 [138] 应用WEPP模型把坡面侵蚀分为细沟侵蚀与细沟间侵蚀,其中,细沟侵蚀模块的细沟侵蚀率是研究人员广泛采用的基础理论公式,由细沟侵蚀率、径流剪切力、土壤抗剪切力的关系式得到土壤的临界抗剪切力。雷廷武等 [139] 通过测定疏松土壤上细沟发生的条件,计算得到临界剪切力与坡度呈线性增加关系。唐泽军等 [140] 进行了REE(rare earth element)示踪土壤侵蚀过程和降雨模拟试验,一系列的试验数据计算表明,试验土壤临界剪应力为1~2Pa,平均值为1.31Pa。在地表水文条件对土壤侵蚀影响的研究中,近些年国内外专家已对土壤侵蚀进行了一系列的试验和模拟,但这些研究多是集中在自由排水条件下,对土壤水分饱和条件下和土壤渗流条件下的研究涉足很少 [28 ~ 32 , 34] 。自由排水条件下的土壤侵蚀与土壤渗流条件下的土壤侵蚀有着本质的区别。Huang等 [29 ~ 31] 和Zheng等 [28 , 34] 的研究中考虑到渗透水对土壤侵蚀的影响,得出在土壤渗流条件下,土壤流失量要比在排水条件下高出3~6倍,却没有结合雨强和径流流量进行进一步研究。
现有成果多集中于研究土壤临界抗剪切力,这为定量研究土壤因子的影响效果奠定了基础。资料中对土壤临界抗剪切力和土壤表面水分供给情况的研究很多,但对土壤初始含水量和土壤特性对溶质迁移过程的影响研究得较少。同时,关于土壤表面凸凹状态对坡面土壤溶质迁移的影响,现有研究成果很多,但对坡面凸凹不平的复杂地表面情况下的研究很少。
地形是影响坡面细沟侵蚀的重要因素之一,坡面位置的不同、地形的差异、坡面坡度的大小、坡长的长短都对水土流失过程产生影响。尽管坡度对细沟侵蚀水流流速的影响一直是具有争议性的问题,但坡度对土壤侵蚀流失量的研究结果较一致。Savat等 [130] 在总结大量有关细沟侵蚀研究的文献后,提出欧洲壤土农地上细沟侵蚀发生的临界坡度为2°~3°,砂壤土细沟侵蚀发生的临界坡度为6°~12°。唐克丽等 [141] 的研究结果表明,凸凹形坡与凹形坡上的土壤流失量均高于直形坡的原因是凸凹形坡与凹形坡易发生浅沟侵蚀,而直形坡一般尚未形成浅沟侵蚀。在其他条件相同的情况下,凸凹形地块的侵蚀量较凹形坡地块的侵蚀量增加了一倍,其中浅沟侵蚀量为总侵蚀量的86.7%。陈永宗 [142] 发现,在5°~30°的坡面上,浅沟条数随坡度的增大而增多,在30°~45°的坡面上,随坡度的增大而减小。刘宝元等 [96] 的野外调查得出,浅沟顶端到分水岭的距离以及集流槽的间距与坡度呈线性相关。郑粉莉等 [143] 发现细沟侵蚀发生的临界坡长与坡度呈非线性关系。张科利 [144 , 145] 指出浅沟发生的临界坡度是18°,认为浅沟发生的临界坡长、间距以及临界汇水面积都随坡度呈二次方变化。靳长兴 [146] 认为水流对坡面侵蚀力的大小与水流所具有的能量成正比,且在流量一定的条件下,当坡度在24°~29°时,水流所具有的能量达到最大,故临界坡度理论上在24°~29°之间。Zhang等 [109] 的研究结果认为,坡度是坡面土壤侵蚀过程中影响最大的因素,它是在土壤侵蚀研究过程中的重要因素。从一个完整坡面来看,坡形可概括为直形坡、凸形坡、凹形坡、凸凹形坡和台阶形坡。杨具瑞等 [147] 根据细沟泥沙动力学建立泥沙起动公式,分析计算得到细沟侵蚀发生的临界坡度公式。邵学军等 [148] 研究发现15°是一个发生细沟侵蚀的特征坡度,并采用经过率定、验证的水动力学模型,用数值计算的方法来给出各种坡面流细沟侵蚀的临界条件。
现有资料多侧重于研究细沟侵蚀过程中的临界坡度,且临界坡度随土壤特性的不同略有不同,而对于漫流剥蚀过程的临界坡度的研究几乎没有,同时,坡面空间位置的变化对水沙迁移量影响的研究也较少。
1)“混合层深度”的概念
径流是土壤养分迁移的主要动力,土壤是相互作用的界面和溶质迁移的“母体”。在通常地表径流或降雨条件下,地表土壤浅薄土层的扰动和土壤溶质的迁移有着密切的关系。1967年,Huff和Kruger [33] 采用放射性悬浮物质模拟土壤溶质的迁移,提出了“有效土壤质量”的概念,首次把径流过程中携带的土壤质量作为研究内容。1973年,Crawford和Donigian [23] 进一步完善了这一概念,并首次提出混合层概念。1975年,Frere等 [60] 在建立ACTMO模型时,通过假设地表径流中土壤溶质浓度同表层土壤中溶质浓度相等,得出混合层深度约为10mm。1977年Donigian等 [22] 开发的CREAMS模型中,假设存在一个低于土壤表面的混合区,雨水、土壤溶液水和渗入水混合瞬间不会发生任何化学过程并直接转移到混合区的下部,其混合过程被假定为彻底且均匀完整。1977年,Donigian等 [22] 描述了土壤溶质随径流迁移的过程,假设降雨过程中雨水与混合层土壤和土壤溶液完全混合,其混合模拟结果表明,混合层中的溶解态化学物质以不同模式存在于混合层的入渗水、径流水和土壤水中。在他们的早期模型中,在土壤表面假设存在一个有效的混合深度0.3cm。1985年,Spencer等 [149] 在加利福尼亚的帝国山谷的几个大的领域,用相同方法检验在地面灌溉径流水域内土壤表面的农药浓度,数据也表明,在沟灌径流水中,农药浓度与地表上层1cm土壤的农药浓度有关。另外,1981年和1983年Ahuja等 [150 , 151] 提出混合层深度为常数,不随时间的变化而变化,混合层中的溶质被按比例分配到各个土壤水分中,包括混合层(包含土壤表面积水层在内)、低于该混合层的入渗层和径流层。混合层的概念基于雨滴动能能加速土壤表面水层的混合和扰动。在一场降雨中,只有土壤表层一定深度以上的溶质才能参与径流损失,该深度被称为有效混合深度(effective depth of interaction, EDI)。1997年Zhang(张勋昌)等 [152] 提出,在降雨过程中,土壤在雨滴打击及径流冲刷等共同作用下,形成一定深度的混合层,见图1-1。
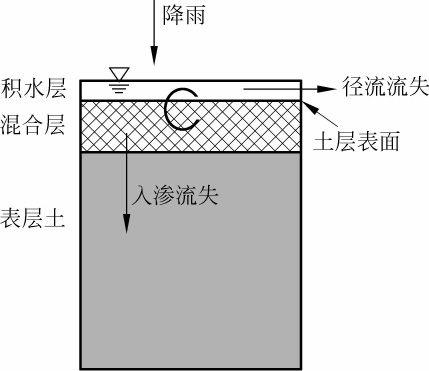
图1-1 完全混合模型概念示意图
混合层内溶质参与径流迁移,而此层以下溶质不参与径流迁移。传统的混合区理论假设土壤表面的地表水下存在一个层,该层内的地表水、土壤溶质和入渗水能够瞬间并且完全混合,该层的土壤溶质没有向下面的土壤层发生迁移。混合层深度或有效的降雨-土相互作用深度是一个很关键的参数,可通过该参数确定土壤溶质流失至地表径流的总量。1989年和1998年,Wallach等 [80 , 153] 提出在土壤表面存在一个完全混合的土层,其有效深度内浓度均匀,被称为“有效迁移深度”,见图1-2。王全九等 [154] 提出了等效径流迁移深度(effective depth of transfer, EDT)的概念,他把土壤有效混合深度分成两部分:一部分称为等效入渗深度;另一部分称为等效径流迁移深度,此深度内的溶质只参与径流迁移,不参与随入渗水的迁移。2004年,Gao等 [79] 研究了雨滴和土壤表面之间的相互作用控制交换层的溶质迁移过程,土壤中溶质从该层离开土壤进入地表径流,假设交换层内溶质充分混合,可以用一个浓度来表示整个层的浓度,见图1-3,土壤溶质迁移概念模型示意图。
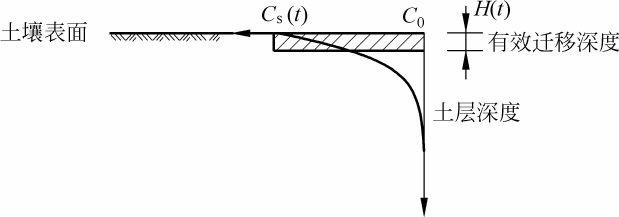
图1-2 有效迁移深度示意图
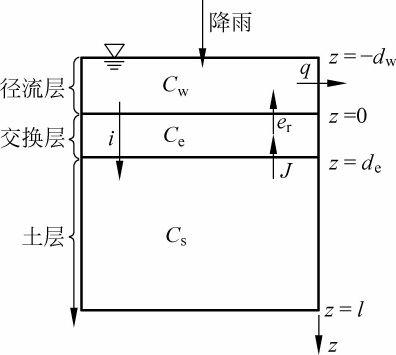
图1-3 土壤溶质迁移概念模型示意图
2)“混合层深度”的量化研究结果及应用
试验研究的结果显示,混合层深度可能小于10mm,一般为2~10mm。1975年,Ponce等 [155] 在研究总溶解盐的过程中,发现径流中浓度与土壤0~2.5mm浓度相近,与0~30mm深处的土层相关性较差。通过模型校正,1977年,Donigian [19 , 20] 发现混合区的深度范围为0~3.2mm。1978年Sharpley等 [156] 、1979年Leonard等 [157] 采用经验值与数理统计相结合的方法,确定土层中0~10mm中的除莠剂参与径流。1980年,该深度被Knisel [91] 编写的美国农业部化学沉积物转移模型收编于农业部管理系统。1981年,Ahuja等 [150] 应用磷32和溴作为示踪剂,发现了混合层平均有效作用深度为2~3mm。Snyder和Woolhiser [158] 的研究中,用水槽与沙及示踪染料作为试验材料,结果表明在渗透条件下有效混合层深度大多小于10mm。在基于完全的和均匀混合的概念基础上,1999年Zhang(张勋昌)等 [78] 的研究表明,在土壤水、渗透和径流发生彻底混合时,混合深度为3~4mm,小于经常被使用在文献和模型中的10mm。同时,他们进一步研究混合层深度,用石膏作为示踪剂,量化土壤溶质的转移过程,通过土壤溶质从下面进入混合区,在零渗透或排水不良的条件,运用这一方法可用于预测化学浓度。土壤溶质从土壤溶液转移到地表径流,可以形容为两种速率的过程:一种为快速过程,只限于混合层范围内(<2~3mm),该层内土壤溶质呈指数递减,即在一个较短的时间内,由于雨滴的扰动,溶质的快递迁移过程使得土壤中的化学物质迅速溶解在土壤表层的混合区中;另一种为缓慢过程,在一个较长的时间内,分子扩散过程和流体力学扩散过程占主导地位,土壤溶质被模拟转移到底层土壤混合层。
另外一些研究学者的试验结果表明,混合层深度要大于10mm。Wang等 [159] 在对土壤中钾元素迁移过程的研究表明,土壤有效作用深度随着雨滴动能的增大而增加,当雨滴动能达到0.459×10 - 3J时,土壤有效作用深度为14.5mm。张兴昌等 [15] 、邵明安和张兴昌 [42] 、张亚丽等 [10 , 11] 在对土壤氮素作用深度的研究中,发现径流与土壤中硝态氮的EDI明显大于铵态氮的EDI,两者之差为7~15cm,同时还发现EDI沿坡面分布存在差异,坡面中下部较深,坡上部较浅。
混合层深度或有效作用深度是非点源污染模型中一个非常重要的参数,因为它可以决定有效的土壤溶质萃取量。混合层概念已被广泛接受,并用来预测化学损失地表径流。在大多数模型中,它的深度都被假设为10mm,如在年非点源污染模型(the annualized agricultural non-point source pollutions, AnnAGNPS) [93] 、流域非点源模型和土壤水文评价工具模型(soil and water assessment tool, SWAT) [160] 中,有效渗透深度或混合层深度都假定为10mm。
3)以“混合层深度”为研究对象的模型的发展现状
(1)混合模型
Ahuja等 [150] 用磷作为示踪剂,研究了降雨、径流、土壤之间的相互作用过程,研究结果表明,表层土壤溶质最有可能迁移至地表径流流失,随着深度的增加,迁移至地表径流的可能性呈指数衰减趋势。在简单的完全混合模型中,Emmerich等 [161] 用模拟土壤表面土壤溶质的转换和迁移过程中的整体式模型和分散式模型对比,预测了土壤溶质浓度迁移过程的浓度变化。以上为充分混合模型的研究,但近几年,学者们又将混合模型进一步完善。2006年,王辉 [162] 利用混合模型反推有效迁移深度,发现土壤溶质不同,其等效迁移深度也不同,硝态氮大于钾元素大于磷元素,其研究结果还发现,等效迁移深度与地表径流中的溶质浓度呈显著正相关;同时还引入土壤侵蚀影响因子,建立了地表径流过程中土壤溶质迁移模型。
(2)确定混合层深度模型
王全九等 [163 ~ 167] 认为,虽然大部分国外学者认为指数函数能够很好地模拟土壤溶质浓度的变化过程,但这种描述对于水土流失地区却不适用,特别是我国特有的黄土坡,并不一定完全适用,该模拟中没有考虑到水土流失加重了土壤溶质的流失。王全九等根据黄土坡的特有地质,研究土壤溶质随地表径流迁移,提出了等效对流质量传递模拟模型。试验结果表明,有效迁移层中的土壤溶质随径流迁移的概率是相等的,有效迁移层中土壤溶质的浓度分布是均匀的,从而提出土壤溶质存在于土壤溶液中。最后,王全九通过试验资料采用指数函数和幂函数,通过率定模型中的参数,对模型进行了初步验证,结果表明,在室内模拟条件下,实测结果与模拟结果比较接近。
(3)对流扩散模型
1983年,Ahuja和Lehmen [151] 利用NaBr作为示踪剂,采用室内人工模拟降雨,研究了土壤溶质迁移至地表径流的流失过程。Ahuja等 [168] 对比研究了常态分子扩散和被降雨加速扩散系数,模拟了降雨加速分子的扩散过程。Zhang(张勋昌)等 [78] 通过采用对3种不同的土壤进行人工降雨模拟试验,用石膏作示踪剂放置在土层下5mm深处。试验结果证明了传统的对流扩散方程的正确性,同时也证明了只有在混合层中的土壤溶质迁移的可能性,研究结果认为,有效混合层厚度(mixing zone depth, MZD)小于4mm。
(4)有效传递深度概念模型
1989年,Wallach等 [80] 提出了有效传递深度(EDT)的概念。王全九等 [154] 提出了土壤中化学物质在降雨-径流过程中流失,它受各种物理、化学、生物过程的控制,同时受土壤颗粒大小、质地、降雨过程、土壤孔隙比、土壤地表植被覆盖及其空间变异性的影响,这些因素的共同作用使土壤溶质的迁移过程变得十分复杂。在实际应用中,主要关心地表径流中化学物质的浓度变化及其流失量,并不需要对溶质迁移过程中复杂的物理化学过程研究过细。所以,将土壤溶质径流迁移的过程作为一个随机迁移过程,便于预测土壤溶质随地表径流迁移的过程。
(5)二层解析模型
童菊秀和杨金忠 [169] 用矢量合成方法,根据土壤表面径流中化学物质流失的流动特征和物理规律,建立了二层解析模型,描述了从降雨开始到径流过程中,土壤中溶质进入地表径流并流失的过程。他们充分考虑了土壤中溶质的入渗和扩散作用,利用非完全混合参数得到表面流失和入渗的合成。基于溶质质量守恒和水量平衡,将土壤混合层和积水径流混合层作为研究对象。