




下面我们简单介绍一下黎曼几何的建立。
欧氏几何,以它逻辑的严密,形式的完备和优美,两千年来为数学家和哲学家所倾倒。使人感到美中不足的是它的第五公设,即平行公理。此公理说,“过直线外的一点,可以引一条、并且只能引一条直线与原直线平行(不相交)”。
与其他公设比较,这个公设显得过长、过于复杂。人们自然希望第五公设能从其他公设推出,从而不再是一个公设。这方面的尝试开始于公元5世纪。一千多年中,许多杰出数学家为它绞尽脑汁,结果都一无所获。
无数前人的失败,终于使后人悟出了道理。第一个察觉其中奥妙的人大概是高斯。然而,由于欧氏几何在数学、哲学和神学中的神圣地位,高斯缺乏公开挑战的勇气,没有发表自己的观点。
最先提出并建立完整的新几何学的是俄国数学家罗巴切夫斯基(1792—1856年)。他是喀山大学的教授。他用“过直线外一点,可以引两条以上直线与原直线平行(不相交)”的新公设来取代第五公设。然而,他的理论在国内无人能懂,多次投稿均被拒绝,俄国彼得堡科学院甚至认为,“罗巴切夫斯基先生这方面的工作谬误连篇,今后不必理睬。”
罗巴切夫斯基只好把论文发表在喀山大学的学报上,外界几乎无人知晓。后来他出国演讲,宣传自己的新几何,但还是遭到冷遇。唯一听懂了他的理论的高斯,未敢公开表示赞同。高斯在日记和给友人的信中写到,会场上,自己大概是唯一听懂了罗巴切夫斯基工作的人。
应该说明,高斯虽然未对新几何表态,却高度评价了罗巴切夫斯基的其他工作。经高斯提名,德国科学院授予罗巴切夫斯基通讯院士的光荣称号。然而,罗巴切夫斯基最杰出的工作,却长期得不到承认。他晚年双目失明,处境凄凉,但仍在学生的协助下,顽强地通过口述完成了自己的工作,并在逝世前,终于得到世界的认可。罗巴切夫斯基的新几何,被称为罗氏几何。
比罗巴切夫斯基稍晚一点,年轻的匈牙利数学家鲍耶(1802—1860年)也独立地研究了这个问题,并提出了与罗氏一样的新几何构想。鲍耶采用了反证法,企图从“第五公设不成立”引出谬误。他假设过直线外的一点可以引两条以上的平行线,试图推出谬误。然而他在反证的路上越走越远,却始终不见“谬误”的影子。鲍耶的思想突然产生了飞跃,认识到可以引入不同于第五公设的其他公理,例如把“过直线外一点可以引两条以上的平行线”作为公理,取代“第五公设”建立新的几何学。
鲍耶的父亲是高斯的同学,他把儿子的工作告诉高斯,征求他的意见。高斯回信说:我实在无法赞扬你的儿子,因为赞扬他就等于赞扬我自己,我早就得到过与他相同的结果。
鲍耶误解了高斯对他工作的评价,以为高斯要借其所处的地位来窃取他的成果,于是愤而终止了自己的研究。幸亏鲍耶的父亲把儿子的研究成果作为附录,收在自己的一本书中出版,否则,鲍耶的成就将无人知晓。
德国数学家黎曼用另一个公设来代替欧几里得的第五公设。他提出,“过直线外一点的任何直线都必定与原直线相交”,也就是说,一条平行线也做不出来。他所建立的几何称为黎氏几何。
实际上,欧氏几何、罗氏几何、黎氏几何描述的是不同曲率的空间(图3-5)。欧氏几何描述零曲率空间(如平面),黎氏几何描述正曲率空间(如球面),罗氏几何描述负曲率空间(如伪球面、马鞍面)。弯曲空间中没有直线。罗巴切夫斯基等人谈论的直线实际是“短程线”,即两点之间的最短线,例如球面上的大圆周。平直空间中的短程线就是直线,短程线可以看作直线在弯曲空间的推广。罗巴切夫斯基等人所说的平行直线,实际上是“不相交的短程线”。
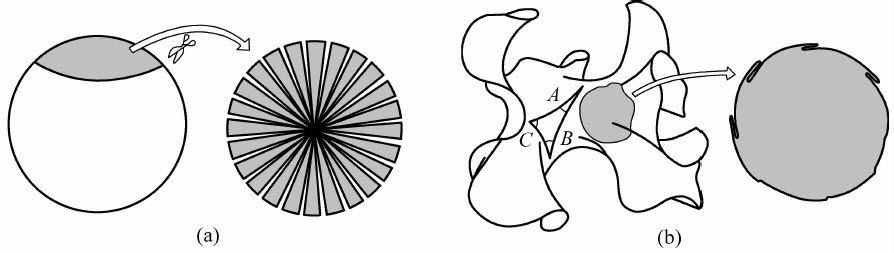
图3-5 正负曲率的二维空间
罗氏几何和黎氏几何,统称非欧几何。黎曼又把欧氏几何与非欧几何合在一起,成为黎曼几何。