




世界科学发展往往是由一个时代的最重要的科学家所引领,他们的名字也因此成为那个时代的里程碑。人们说17世纪是牛顿的时代,18世纪无疑属于欧拉,那时欧洲各国数学家们谈论的都是“欧拉的数学”。欧拉是18世纪科学的领军人物,名声已经传遍欧洲大陆。在伊万诺夫娜女皇退位后,普鲁士国王腓特烈盛情邀请欧拉到柏林科学院担任数理学院院长,宫廷数学家,并兼任公主安哈特·蒂苏的老师。
普鲁士王太后对诚恳老实、稳重谦逊、淳朴温和的欧拉颇具好感,喜欢和欧拉聊聊天,但却谈不起来,因为欧拉非常紧张,只是用“是”与“否”回答王太后。王太后不解,这位举世闻名的大学者何以如此谨言慎行?欧拉回答说:“我在那样一个国家居住了十几年,那里的人若是说错了话就会被吊死。”
腓特烈国王年轻时数学读得很费劲,也不喜欢数学家,但非常支持数学研究,也敬重欧拉,因为他知道数学是一门很难学但很有用的学问,欧拉又是个绝顶聪明的人。腓特烈对哲学情有独钟,更喜欢结交有名的哲学家,法国启蒙主义思想家伏尔泰曾是腓特烈的座上宾。有一次欧拉奉命作陪,伏尔泰口若悬河,长袖善舞,取悦腓特烈。他言谈话语中不断夹杂着欧拉听不懂的名词。欧拉生性谦恭,不善应酬,无法与其周旋。腓特烈却认为欧拉孤陋寡闻,不能当宫廷科学院的头面人物,并因此萌生了要撤换欧拉数理学院院长的念头,他想到了法国大数学家达朗贝尔。
达朗贝尔是“偏微分方程”这一学科的创始人,也是世界上第一部影响巨大的百科全书的副主编,担任数理学院院长当然够格。但是达朗贝尔直率地拒绝了腓特烈国王,并且说:“没有任何数学家的地位可以在欧拉之上。”
“不要人夸颜色好,只留清气满乾坤。”尽管饱受国王冷眼与排斥,欧拉丝毫不减他对数学的热忱,执掌了普鲁士数学界长达25年,那也是德国历史上数学最辉煌的时期。他在柏林期间的研究领域非常宽泛,尤其在微分方程、曲面微分几何等方向上,进行了开拓性的探索。此外在物理与力学方面,如行星运动、刚体运动、热力学、弹道学等学科的研究上,也取得了重大的突破性成就。
欧拉重视数学教育,虽然没有很多机会亲自授课,但写过许多通俗生动的数学读物。他还特意为青少年写过一本书《给德国公主的信》,其中谈到对物理、数学乃至所有科学的思维、语言文字乃至文学、真理乃至信仰的看法。
欧拉自始至终固守他那来自基督教家庭、自幼就建立起来的信仰。尽管非常不喜欢抛头露面,又不善言辞,可是一旦遇上那些大牌哲学家鼓吹无神论,欧拉就如勇士一般,冲上前去,与之辩论。有趣的是,欧拉在辩论中所使用的论据都是取自他最熟悉的数学。
休谟是位英国的哲学家和历史学家,同时也是位外交官,曾出使法国,后来还当上了英国的副国务大臣。他是经验主义哲学的代表人物,其著作如《人性论》和《自然宗教对话录》等对后世颇有影响。1765年前后,休谟在担任驻法大使临时代办期间,四处宣讲,批判所谓“宇宙设计论”,给予基督教沉重的打击。休谟的无神论基本观点是:因为无人能从物质上或理性上证明上帝的存在,所以上帝根本不存在,那仅仅是某些人信仰的对象罢了。
休谟曾游历普鲁士,不忘宣讲他的无神论。欧拉公开挑战,反驳休谟,颇为有趣:
“你知道什么是-1的平方根(即
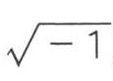 )吗?它既看不见也摸不着,这个数字既不等于0,也不大于0,也不小于0。按照你的逻辑,你该说:-1的平方根是不存在的物质,所以数学里不该有它。但是,如果没有负数的开平方,就不可能把12分解成两个数字之和,其乘积等于40[注:12=(6+
)吗?它既看不见也摸不着,这个数字既不等于0,也不大于0,也不小于0。按照你的逻辑,你该说:-1的平方根是不存在的物质,所以数学里不该有它。但是,如果没有负数的开平方,就不可能把12分解成两个数字之和,其乘积等于40[注:12=(6+
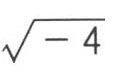 )+(6-
)+(6-
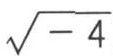 )]。世界上看不见的,却深深存在于我们意识里的事物太多了,你知道吗?即使我们无法用物质去证明-1的平方根之存在,事实上它却存在着,否则数学都不存在了。因此,你所说‘无法用物质证明其存在的,其实就是不存在的’,这是大错特错!让我告诉你:上帝依然存在,即使无法用物质去证明。”
)]。世界上看不见的,却深深存在于我们意识里的事物太多了,你知道吗?即使我们无法用物质去证明-1的平方根之存在,事实上它却存在着,否则数学都不存在了。因此,你所说‘无法用物质证明其存在的,其实就是不存在的’,这是大错特错!让我告诉你:上帝依然存在,即使无法用物质去证明。”
难怪人们说欧拉像一只鸟,靠着双翼在天空翱翔,一翼是数学,另一翼则是信仰。也许人们更该惊叹约翰·伯努利教授的先见之明,欧拉真的可以称得上是“数学家中的神学家”!
虽然欧拉没有成为一位专职传道人,但他笃信基督。那浸润在灵魂深处的信仰,赋予了欧拉一颗仁爱宽厚之心。欧拉品格高尚,为人谦卑,即使在成为举世瞩目的大数学家后。他不忘师恩,继承和发扬了大师风范,在成为举世闻名的大数学家之后,提携培育新人,不遗余力,以使科学事业薪火相传。他用生动的语言编写了大量的数学书籍,旨在吸引和培育有才华的青年,引导他们步入数学的殿堂。不仅如此,欧拉胸怀宽广,亲手提携后起之秀,例如,他栽培大数学家拉格朗日成名的故事,在数学史上传为美谈。

受欧拉栽培提携的大数学家拉格朗日,是变分法等数学分支的开创者
当时19岁的法国后起之秀拉格朗日曾与欧拉通信讨论“等周问题”,这个问题属于一类所谓“广义极值”的问题。这类问题的研究与解决导致产生了一个新的数学分支“变分法”。这名词就是欧拉定的,当时他也在研究这一类问题。“广义极值”问题更早可以回溯到牛顿、莱布尼茨和伯努利的时代。当年,约翰·伯努利提出那个著名的“最速降线问题”,挑战其他数学家,可看做是“变分法”的起源。欧拉同拉格朗日一样,也找到了解决这类问题的一般方法,但他故意压下自己的论文,而让拉格朗日率先发表其研究成果。拉格朗日成为“变分法”的开创者,一举成名。后世的数学家们明白了真相,如今的教科书里公正地称欧拉和拉格朗日都是“变分法”的创始人:“变分法”中的基本方程就以欧拉的名字命名,“变分法”中的一条非常基本与重要的定理则被称为欧拉一拉格朗日定理。