




本书的具体安排如下:
第2章,为求解线性矩阵时标动力学方程的解,我们给出了时标上广义常矩阵指数函数的算法及显式表达式。
第3章,我们将时标上广义实值指数函数的定义推广到更一般的有单位元Banach代数中,我们定义的指数函数恰为交换Banach代数中的线性时标动力学方程的唯一解。
第4章,我们考虑了Banach空间中的线性时标动力学方程(1.2.2)解的存在唯一性。在一定意义下找到了Banach空间中的一个最大的有界线性算子类,使得时标上线性动力学方程解的存在唯一性不依赖于具体时标。我们还在Hilbert空间中刻画了该算子类的大小。
第5章,我们对复时标上的解析函数进行了初步研究。讨论了函数在复时标上的解析性与经典解析性之间的关系,得到了两类复时标上的解析函数可局部开拓为经典解析函数的充要条件。并且还讨论了单项式
 在复时标上的解析性,对
n
=3,
n
=4的情况得到了部分结果。
在复时标上的解析性,对
n
=3,
n
=4的情况得到了部分结果。
在本书的第2章中,我们主要考虑时标上的线性常矩阵动力学方程

其中
A
为
m
阶常矩阵,
 为矩阵值函数。
为矩阵值函数。
不失一般性,假设时标
 包含坐标原点。我们得到了方程(1.4.1)的解关于矩阵
A
的多项式表达形式,并且通过求解纯量线性动力学方程求得了多项式的系数函数。
包含坐标原点。我们得到了方程(1.4.1)的解关于矩阵
A
的多项式表达形式,并且通过求解纯量线性动力学方程求得了多项式的系数函数。
设 ω 是一个能被 A 的极小多项式整除的首一多项式。不妨设

其中 b 0 =1。
称初值问题

的解为与 ω 相伴的动态解 ,其中 D 代表Δ导算子。
定义 ω 的 Horner多项式 为

我们利用纯量方程(1.4.3)的解将矩阵方程(1.4.1)的解表示成 A 的多项式。
定理1.4.1(主要定理1)
设
 为
ω
的Horner多项式;
f(t)
是与
ω
相伴的动态解。则矩阵方程(1.4.1)的解(即广义常矩阵指数函数)为
为
ω
的Horner多项式;
f(t)
是与
ω
相伴的动态解。则矩阵方程(1.4.1)的解(即广义常矩阵指数函数)为

由(1.4.4)和(1.4.5)可见,广义常矩阵指数函数的系数完全由与
ω
相伴的动态解
f(t)
决定。为得到
f(t)
的结构,首先定义
 到
到
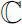 上的多项式序列
上的多项式序列

其中
 是时标动力学方程
是时标动力学方程
 的解。
的解。
定义时标
 上的基本广义指数多项式为
上的基本广义指数多项式为

定义可交换的卷积运算
 为
为

其中

我们得到了与 ω 相伴动态解的显式表达式。
定理1.4.2(主要定理2) 设 ω 同(1.4.2),令

则 fω 是与 ω 相伴的动态解。
由定理1.4.1和定理1.4.2可得方程(1.4.1)的解即广义常矩阵指数函数的显式表达。
对于时标上线性常矩阵▽动力学方程的求解问题,我们可以得到与方程(1.4.1)平行的结论。
对于时变动态系统(1.2.6)(即 A ( t )未必是常函数),解的结构比较复杂。
我们知道,由
μ-
柱面变换定义的实值Δ指数函数
 是纯量方程(1.2.5)的解。
是纯量方程(1.2.5)的解。
在本书的第3章,我们将实值Δ指数函数的定义推广到一般的有单位的Banach代数中,得到了Banach代数中
 的表达式。并且证明对于交换的Banach代数,我们定义的Δ指数函数恰为时标动力学方程(1.2.6)的唯一解。
的表达式。并且证明对于交换的Banach代数,我们定义的Δ指数函数恰为时标动力学方程(1.2.6)的唯一解。
设
A
是Banach代数
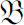 中的元素,定义
A
的谱为
中的元素,定义
A
的谱为

 ;
A
的预解集为
;
A
的预解集为
 ;
A
的谱半径为
;
A
的谱半径为
 [33]
。记
[33]
。记

由Riesz函数演算得,当
 。
。
设函数
 右稠连续,在3.2节,我们在一定条件下,利用函数演算定义了算子值函数
A
(·)的
μ-
柱面变换。
右稠连续,在3.2节,我们在一定条件下,利用函数演算定义了算子值函数
A
(·)的
μ-
柱面变换。
定义1.4.1
设
 是时标,
G
是解析函数
Logz
的单值解析分支。若函数
A
(·)的谱满足条件
是时标,
G
是解析函数
Logz
的单值解析分支。若函数
A
(·)的谱满足条件

则定义函数 A (·)的 μ- 柱面变换为

进而,我们利用 μ- 柱面变换引入Banach代数中Δ指数函数的概念。
定义1.4.2
设
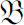 为有单位元的Banach代数(或其子代数),
为有单位元的Banach代数(或其子代数),
 为时标,函数
为时标,函数
 。若函数
A
(·)右稠连续且满足定义1.4.3中的谱条件(
S
),则可以定义函数
A
(·)的Δ指数函数为
。若函数
A
(·)右稠连续且满足定义1.4.3中的谱条件(
S
),则可以定义函数
A
(·)的Δ指数函数为

在3.3节,我们证明了定义1.4.4中的Δ v 指数函数是有单位元的交换Banach代数中方程(1.2.6)的唯一解,推广了纯量方程的结果。
定理1.4.3(主要定理3)
设
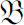 是有单位元的交换Banach代数(或其交换子代数),
I
为
是有单位元的交换Banach代数(或其交换子代数),
I
为
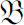 中的单位元。若
A
(·)为
中的单位元。若
A
(·)为
 到
到
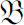 上的右稠连续函数且满足谱条件(
S
),则
上的右稠连续函数且满足谱条件(
S
),则
 是方程(1.2.6)的唯一解。
是方程(1.2.6)的唯一解。
我们在3.4节考虑Banach代数中的▽指数函数,用类似的方法得到了与定理1.4.4和定理1.4.5平行的结论。
在本书的第4章,我们考虑了Banach空间中的时标线性动力学方程(1.4.3)解的存在唯一性问题。在4.1节,我们定义
B
(
X
)中的算子类
 ,并且证明
U
是在一定条件下保证系统(1.2.3)解的存在唯一性不依赖于时标的最大算子类。
,并且证明
U
是在一定条件下保证系统(1.2.3)解的存在唯一性不依赖于时标的最大算子类。
定理1.4.4(主要定理4) U 是 B ( X )中满足下面条件( G )的最大的算子类。
(
G
):对任意的时标
 ,若算子值函数
,若算子值函数
 按强算子拓扑右稠连续,则齐次方程(1.2.3)必存在唯一的全局解。
按强算子拓扑右稠连续,则齐次方程(1.2.3)必存在唯一的全局解。
在4.2节,我们用算子逼近的工具,在Hilbert空间中刻划算子类
U
的闭包和内部。设
 ,
N(A)
和
R(A)
分别表示
A
的核空间和
A
的值域。称
,
N(A)
和
R(A)
分别表示
A
的核空间和
A
的值域。称
 是一个semi-Fredholm算子,如果
R(A)
是闭的,而且nul
A
和nul
A
*中至少有一个是有限的,其中
是一个semi-Fredholm算子,如果
R(A)
是闭的,而且nul
A
和nul
A
*中至少有一个是有限的,其中
 ;此时
;此时

 称为
A
的指标。定义算子
A
的Wolf谱为
称为
A
的指标。定义算子
A
的Wolf谱为

 ,称
,称
 为
A
的semi-Fredholm域。对任意的
为
A
的semi-Fredholm域。对任意的

 设
F
为
B(H)
的子集,用
设
F
为
B(H)
的子集,用
 表示集合
F
的闭包,
表示集合
F
的闭包,
 表示
F
的内部。
表示
F
的内部。
定理1.4.5(主要定理5)
设
 ,则有
,则有
(i)
 ,当且仅当对任意
,当且仅当对任意


(ii)
 ,当且仅当
,当且仅当

可见算子类
U
有内点,因此含有较多的算子。作为推论,当
B(H)
=
M
m
为矩阵代数时,
 ,即
U
在
M
m
中稠密。
,即
U
在
M
m
中稠密。
在4.3节,类似与Δ动力学方程,我们讨论了线性▽动力学方程解的存在唯一性问题。得到了与定理1.4.6和定理1.4.7平行的结论。
在本书的第5章,我们主要考虑函数的Δ(和▽)解析性与经典解析性的关系。在5.2节,我们讨论了几类复时标上Δ(和▽)解析函数的局部开拓条件。
设
 上的Δ(或▽)解析函数。对
上的Δ(或▽)解析函数。对

 ,若存在复平面上的邻域
,若存在复平面上的邻域
 内的经典解析函数
g
(
z
),使得对任意的
内的经典解析函数
g
(
z
),使得对任意的
 ,都有
,都有
 ,则称
g
(
z
)为
f
(
z
)在点
z
0
的局部解析开拓。若对任意
,则称
g
(
z
)为
f
(
z
)在点
z
0
的局部解析开拓。若对任意
 都存在局部解析开拓,则称Δ(或▽)解析函数
f(z)
在
都存在局部解析开拓,则称Δ(或▽)解析函数
f(z)
在
 上存在局部解析开拓。
上存在局部解析开拓。
我们对实轴平行线组成的复时标上解析函数的局部解析开拓进行了研究。
设
G
是
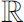 的一开子集,称映射
的一开子集,称映射
 是实解析的,如果对每一点
是实解析的,如果对每一点
 ,都存在以
a
为中心的开邻域
,都存在以
a
为中心的开邻域
 ,使得在
U
中,
f(x)
等于关于变量
x
-
a
的绝对可和幂级数的和
[37]
。
,使得在
U
中,
f(x)
等于关于变量
x
-
a
的绝对可和幂级数的和
[37]
。
定理1.4.8(主要定理6)
设
 上的闭区间(可以是
上的闭区间(可以是
 中不含聚点的至多可数集合,其中
中不含聚点的至多可数集合,其中

 。设函数
。设函数
 上Δ解析,且
上Δ解析,且

 。则
。则
 的实部
的实部
 与虚部
与虚部
 在(
a,b
)内实解析,当且仅当
f(z)
在
在(
a,b
)内实解析,当且仅当
f(z)
在
 上存在唯一的局部解析开拓
上存在唯一的局部解析开拓

 。
。
与Δ解析函数类似,我们研究了▽解析函数的局部解析开拓。
在5.3节,我们对单项式 p n (z) = z n 在复时标上的Δ和▽解析性进行讨论,得到一些结果。
定理1.4.7(主要定理7)
设
 上的两个时标。对任意给定的自然数
n
≥3,若
上的两个时标。对任意给定的自然数
n
≥3,若
 中存在右散点,
中存在右散点,
 中至少存在
n
个右稠点。则单项式
中至少存在
n
个右稠点。则单项式
 上存在不Δ解析的点。
上存在不Δ解析的点。
定理1.4.8
当
n
=3时,设
 上的时标,并设
上的时标,并设
 分别为
分别为
 中全体右散点组成的集合,则
中全体右散点组成的集合,则
 上至多存在一个Δ解析点
上至多存在一个Δ解析点
 ,且满足
,且满足
 ;
;
 。
。
定理1.4.9
当
n
=4时,设
 上的时标,若
上的时标,若
 中存在右散点,
中存在右散点,
 是以
y
0
为极限的单调上升(或下降)数列。则
是以
y
0
为极限的单调上升(或下降)数列。则
 上存在不Δ解析的点。
上存在不Δ解析的点。
对于▽解析函数,我们得到了与Δ解析函数平行的结论。