下载掌阅APP，畅读海量书库
立即打开
复变函数最早起源于16世纪中后期的复数理论，研究的中心对象是所谓解析函数，因此复变函数论又称为解析函数论，简称函数论 ［99］ 。
20世纪四五十年代，为研究解析函数在高斯整数集（Gaussian integers）
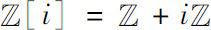上的类似物，Isaacs，Ferrand和Duffin分别从不同角度建立了离散解析函数理论。
1941年，Isaacs
［59］
用复变函数中的Cauchy-Riemann方程在
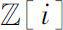上的两种差分形式定义了两类全纯函数。设
E
是
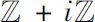的子集，且满足对任意的
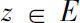，都有
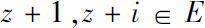。称函数
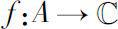是
E
上的第一类单差函数（monodiffric functions of the first kind），若
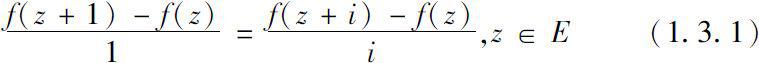
称函数
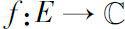是
E
上的第二类单差函数（monodiffricfunctions of the second kind），若
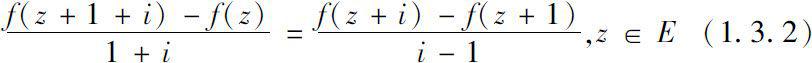
Isaacs在文献［ 60 ］中对第一类单差函数做了进一步的研究。近期关于这类函数的研究可参见文献［ 84 ， 69 ］。
1944年，Ferrand ［44］ 对第二类单差函数进行研究（亦可参见文献［ 45 ］），并称其为预全纯函数。
1956年，Duffin ［40］ 将第二类单差函数称为离散解析函数，并进一步研究了它的性质。关于这类离散解析函数的后续研究结果也很丰富 ［ 66 ， 14 ， 81 ， 68 ］ 。
为方便，本书采取Duffin的叫法，称第一类（或第二类）单差函数为“第一类（或第二类）离散解析函数”。
称复平面上间隔均匀且平行与实轴的直线构成的集合为“半格”，定义域为半格的单值函数称为“半离散的” ［71］ 。
1963年，Kurowski ［71］ 定义解析函数在半格上的两种类似物。分别称函数 f 为第一类和第二类半离散解析函数，若 f 分别满足差分形式
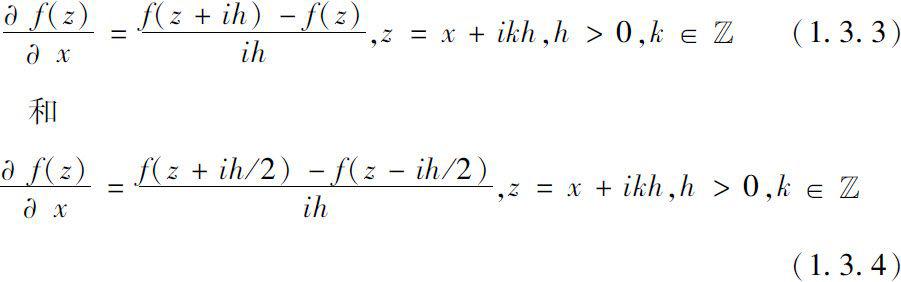
Kurowski对半离散解析函数进行了比较系统的研究 ［ 72 ， 72 ， 74 ， 75 ， 76 ］ 。
以上为离散和半离散复分析理论发展的概况。
继Hilger于1988年提出时标理论之后，许多单变量连续分析和离散分析的概念都推广到时标上来（如§1.1节所述）。关于时标上多元函数的研究开始于Ahlbrandt、Morian ［4］ 及Hoffacker ［55］ 对时标上偏微分方程的研究。
2004年，Bohner和Guseinov在文献［ 17 ］系统地研究了时标上多元函数的微分计算，为后来人们研究时标上的多重微积分 ［ 18 ， 86 ， 20 ， 6 ， 85 ］ 及偏微分方程 ［ 85 ， 85 ］ 等领域奠定了基础。
2006年，Bohner和Guseinov
［19］
首次将连续和离散复分析推广到时标上。他们定义了任意时标复平面（或复时标）
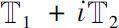上的Δ解析函数（其中
为任意时标）。
令
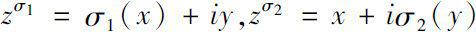。下面介绍复时标上复值函数Δ解析的概念。
定义1.3.1
［19］
设
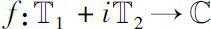为复值函数，对
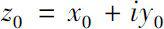
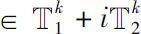，若存在一个复数
B
及
δ
＞0，使得对任意的
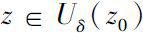
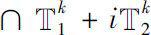（其中
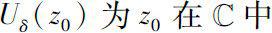的
δ
-领域），都有
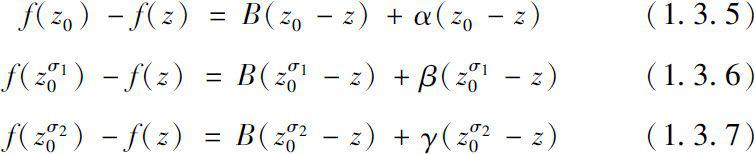
其中
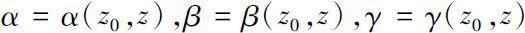都在
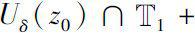
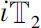上有定义，
在
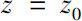点的函数值都为零，且满足
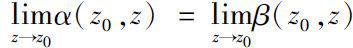
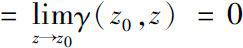。那么称
f
在
z
0
点Δ解析（或Δ可微），称复数
B
为
f
在
z
0
点的Δ导数，记为
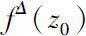。若
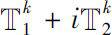上任一点都Δ解析，则称
f（z）
在复时标
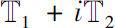上Δ解析。
当
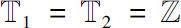（或
，
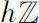h
为非零常数）时，Δ解析函数即为第一类离散解析函数
［59］
；当
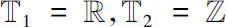时，即为第一类半离散解析函数；当
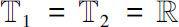时，即为经典复分析中可微函数。因此，复时标上的Δ解析函数将第一类离散和半离散解析以及经典解析的概念统一并推广到时标框架下。文献［
19
］还得到了复时标上Δ解析函数的Cauchy-Riemann条件，定义了复时标上复变函数的积分并且在水平和竖直的折线段上得到了时标版本的Cauchy积分定理。
2007年，Sinan
［63］
定义了复时标
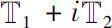上的▽解析函数，并将文献［
19
］的结果推广到▽解析函数的情形。
复时标上的Δ和▽解析函数与离散、半离散解析函数以及经典解析函数的差别很大，本书将在第5章考虑复时标上函数的Δ和▽解析性，通过讨论一些特殊复时标上的解析函数何时能局部扩张为经典解析函数，来研究Δ和▽解析函数与经典解析函数之间的异同之处。我们还将讨论单项式
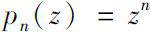在复时标上的解析性。