1.2　时标上的线性动力学方程

本节将从三个方面介绍抽象空间中线性时标动力学方程的研究进展。首先引入Banach空间中时标动力学方程解的存在唯一性问题，然后介绍时标上矩阵动力学方程求解的问题，最后给出Banach代数中的线性时标动力学方程。

Hilger ^［52］ 首先在Banach空间中考虑了非线性动力学方程

其中 f （·，·）是 到 X 上的函数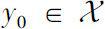， 。得到了Banach空间中时标动力学方程解的存在唯一性定理（亦可参见［ 53 ］或［ 23 ］）。

作为推论，可以得到线性Δ动力学方程

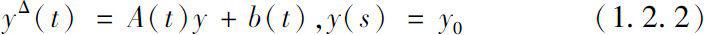
全局解的存在唯一性定理。（其中 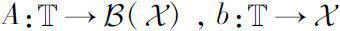）。为方便介绍方程（1.2.2）解的存在唯一性定理，先介绍一下二元函数 f 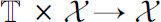： 的右稠连续及回归的定义（注意与前面一元函数的定义加以区别）。

定义1.2.1 （ ^［23］ ）

（i）若对任意的连续函数 ，都有函数 g ( t )＝ f （ t ， x （ t ））右稠连续，则称二元函数 f （·，·）是右稠连续的；

（ii）设 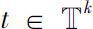，若映射 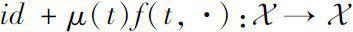可逆，则称 f （·，·）在点 t 处 μ -回归。

其中， id 是 X 到 X 的恒等映射）。若 f （·，·）在任意的 xf （·，·）处都 μ -回归，则称 f （·，·）在 上 μ -回归。

引理1.2.1 ^［52］ 若 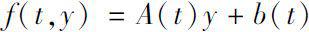在 上 μ -回归且右稠连续，则方程（1.2.2）存在唯一的全局解 。

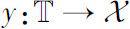由引理1.2.1知，对方程右端函数 A （ t ）和 b （ t ）要求的条件，既依赖于具体时标，又依赖于函数的值域。那么，当方程（1.2）满足什么条件时，其解的存在唯一性不依赖于时标的选取呢？当 b （ t ）＝0时，我们可以将以上问题纳入到算子代数 B （ X ）中考虑。

对于时标动力学方程

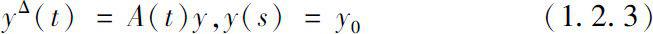
其中 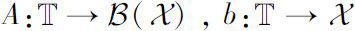。只需考虑算子值函数 A （ t ）即可。由此我们可以提出以下问题：

是否存在 B （ X ）中的算子类 A ，使得对任意时标，若函数 A （ t ）的值域包含在算子类 A 中，则方程（1.2.3）必存在唯一的全局解？

本书将在第4章考虑以上问题并在Hilbert空间中考虑与之相关的算子类。

众所周知，对于 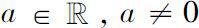，一阶常系数线性微分方程

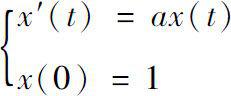
的解为指数函数 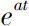。下面我们介绍时标上的线性动力学方程及指数函数之间的关系。

1990年，Hilger ^［52］ 利用柱面变换将指数函数 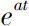推广到一般的时标上。本书总假设 Log （ z ）为主对数函数，其解析区域为负实轴割破的复平面。

对

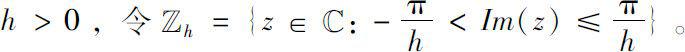
对

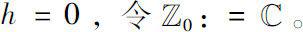
对 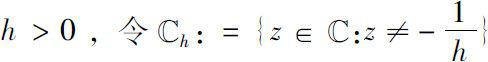，定义 μ -柱面变换 ：

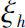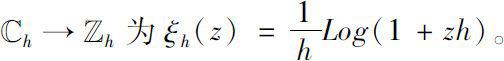
对 h ＝0，定义 。

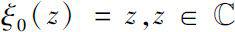称函数 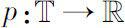为 μ -回归的，若 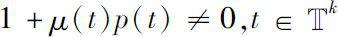。所有 μ -回归且右稠连续的函数 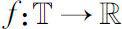所构成的集合记为 。

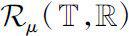设 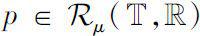，定义时标 上的Δ指数函数为

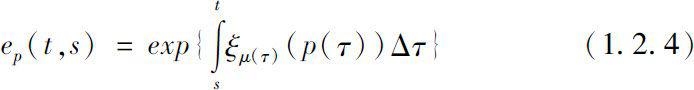
对初值问题

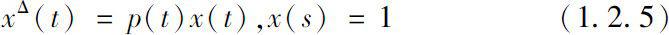
有以下结论。

定理1.2.1 ^［23］ 设 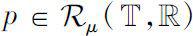，则方程（1.2.5）存在唯一解，且为Δ指数函数 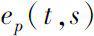于Δ指数函数 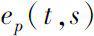的性质可参见文献［ 54 ， 23 ］。Δ指数函数在求解时标上的一阶线性动力学方程，二阶常系数线性动力学方程以及Euler-Cauchy动力学方程中都起到十分重要的作用 ^{［ 24 ， 25 ］} 。类似地，时标上的▽指数函数也有与定理1.2.1平行的结论 ^［7］ 。

考虑时标上的线性动力学方程

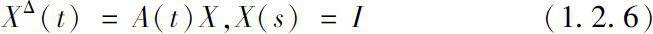
若方程（1.2.6）为矩阵代数 M _m 中的动力系统，则可以作为模型来描述许多力学系统、电路回路系统、生物系统以及生产库存等问题 ^{［ 23 ， 10 ］} 。因此对方程（1.2.6）的解公式及结构的研究具有重要的理论及实际意义。

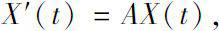
我们知道矩阵指数函数 e ^At 线性微分动力学方程 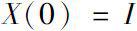的解，且具有无穷级数形式

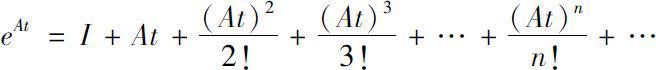
2001年，Bohner和Peterson ^［23］ 直接将方程（1.2.6）的唯一解定义为时标上的广义矩阵指数函数。

定义1.2.2 ^［23］ 若 m 阶矩阵值函数 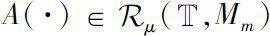，则称线性动力学方程（1.2.6）的唯一解为广义矩阵指数函数，记为 。

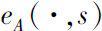关于广义矩阵指数函数的基本性质参见文献［ 23 ］。

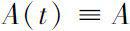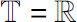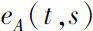
若 为常值函数，当 时，常矩阵指数函数 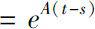。当 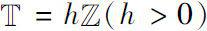且 I ＋ hA 可逆时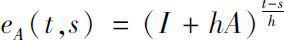， 。关于 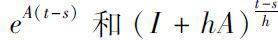的结构及计算方法的研究一直备受数学家们的关注并且取得了丰硕的成果 ^{［ 67 ， 82 ， 83 ， 35 ， 91 ， 13 ］} 。

近些年来，随着时标动力学方程理论的蓬勃发展和应用的需要，人们对广义矩阵指数函数 的结构及算法的研究也取得了一些成果。其中大量研究方法和结果都包含并推广了经典矩阵指数函数的相关结论。

对于常矩阵 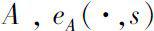的结构相对容易处理，并且许多实际问题最后都可以转化为常矩阵形式。因此近几年，关于 的结构和计算方法的研究备受关注。人们将经典指数函数 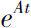的Putzer算法，Harris算法以及Leonard提出的初等算法推广到矩阵指数函数 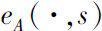的计算中。

1966年，Putzer ^［88］ 为避免求矩阵的Jordan标准型，利用特征多项式等技巧给出了一种方法，得到了矩阵指数函数 e ^At 的一种显式表达式，这种方法被称为Putzer算法。Putzer算法后来被推广到其他矩阵函数的计算中。1991年，Kelley和Peterson ^［65］ 将Putzer算法推广到矩阵的幂 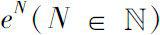的计算中。2003年Ahlbrandt和Ridenhour ^［5］ 应用Putzer算法计算矩阵对数函数 Log （ I ＋ At ）。更多关于Putzer算法的应用可参见［ 41 ， 80 ］。2001年，Bohner和Peterson ^［23］ 将Putzer算法推广到广义常矩阵指数函数的计算中，统一了［88］和［65］中的结果。

2001年，Harris，Fillmore和Smith ^［49］ 提出Harris算法计算矩阵指数函数，得到了 e ^At 的一种显式表达式，Harris算法蕴含了Putzer算法。

2003年，Bodine和Lutz ^［15］ 将Harris算法应用到广义常矩阵指数函数的计算，推广了文献［ 23 ］中的结果。

1996年，Leonard ^［78］ 提出一种初等且有效的方法计算矩阵指数 e ^At ，只需要用到线性齐次常系数微分方程的知识及Cayley-Hamilton定理，当矩阵 A 不可对角化时，该方法尤其适用，且比Harris和Putzer算法更简单实用，适合初学者及工程专业人员。

1998年，Kwapisz ^［77］ 用类似的方法计算 A ^N 。

2006年，Zafer ^［95］ 将Leonard的方法推广到广义矩阵指数函数的计算，后来又将文献［ 95 ］中的方法进行简化 ^［96］ 。Zafer统一并推广了文献［ 78 ， 77 ］中的结果，得到了比文献［ 23 ， 15 ］更初等、更实用的方法计算广义常矩阵指数函数。

2007年，Verde-Star ^［92］ 用初等方法和算子恒等式求解常系数线性矩阵微分方程，将矩阵指数函数的计算转化为对应的纯量齐次微分方程求解问题，得到了 e ^At 关于矩阵 A 的多项式表达。文献［ 92 ］还用类似的方法求解线性矩阵差分方程。

本书将文献［ 92 ］的方法推广到求解时标上的线性矩阵动力学方程。将矩阵指数函数的计算转化为时标上纯量齐次动力学方程求解问题，并得到了纯量动力学方程解的结构，从而得到了广义常矩阵指数函数的显式表达式。

当 A （ t ）为一般的向量值函数时，方程（1.2.6）解 的表达式比较复杂。现有关于 表达式的研究结果中， A （ t ）皆为有限维矩阵值函数 ^{［ 1 ， 34 ］} 。2004年，Adamec ^［1］ 对时标 加了一定限制，并根据系统（1.2.6）构造了对应的微分方程。该微分方程的解在时标 上的限制即为系统（1.2.6）的唯一解。2005年，Da-Cunha ^［34］ 通过构造广义的Peano-Baker级数，得到了 的无穷级数表示。对 A （ t ）为常值函数的情形，分别利用Laplace变换和Cayley-Hamilton定理，得到了广义常矩阵指数函数的两种不同形式的多项式表达。

本书将在第3章中定义有单位元Banach代数中的广义指数函数，从而得到了交换Banach代数中线性时标动力学方程（1.2.6）解的一种显式表达。

g2KhBHE6lS1zsSU+ZsDISG5hjz4UrsMh4gUuCR4VNYduey7bIrZ6Bgy/sUTjSXnA