




人们在研究微分方程和差分方程时发现,二者有很多类似的研究方法及性质。1988年,德国数学家Hilger在他的博士论文
[51]
中建立了时标分析理论。时标即实数轴
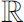 上的任意非空闭子集,例如
上的任意非空闭子集,例如
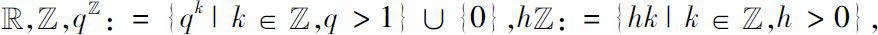 Cantor
集。
Cantor
集。
时标微积分把对微分方程和差分方程的研究统一并推广到时标动力学方程的框架下进行,不仅可以避免对微分方程和差分方程的重复研究,又可以揭示微分方程和差分方程的本质区别 [ 52 , 11 , 12 ] 。不仅如此,时标动力学方程还具有很强的应用价值,在信息、控制、电力系统、经济以及生物学等领域都有广泛的应用 [ 23 , 10 , 19 ] 。例如,一类种群的数量在一个季节是连续变化的,而在另一个季节由于它们的卵处于休眠状态,这时种群的数量为零。在新的季节来临时,卵就会被孵化变成新的生命,形成一个不交叠的种群数量关系。描述这类具有冬眠(或蛰伏)特性的种群数量随季节变化的规律时,在时标
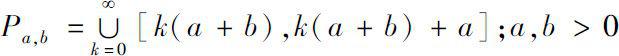
上建立动力学模型更能反映实际情况 [23] 。
近年来,时标微积分理论一直备受关注,取得了大量的研究成果,主要包括时标基本理论及时标动力学方程的研究 [ 26 , 23 ] 。
为方便,先介绍一下时标理论的基本概念。设
 为一时标,定义时标
为一时标,定义时标
 上的前跃算子
上的前跃算子
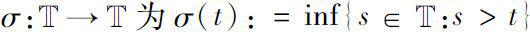 ;后跃算子
;后跃算子
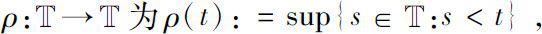
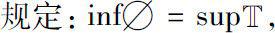
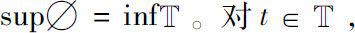 ,定义函数
,定义函数
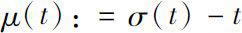 及函数
及函数
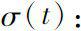
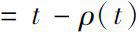 。如果
。如果
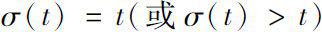 ,则称
t
是右稠的(或右散的);若
,则称
t
是右稠的(或右散的);若
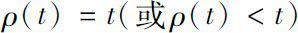 ,则称
t
是左稠的(或左散的)。
,则称
t
是左稠的(或左散的)。
 中的闭区间
中的闭区间
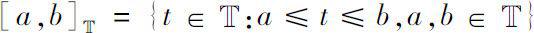 。类似地,可以定义
。类似地,可以定义
 中的开区间和半开半闭区间。由
中的开区间和半开半闭区间。由
 可定义集合
可定义集合
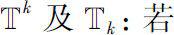
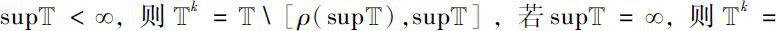
 若
若
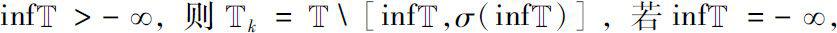
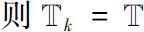 。
。
Hilger首先给出时标上实值函数可微的定义,然后又将可微的定义推广到Banach空间中的向量值函数 [ 52 , 23 , 9 ] 。我们知道,实数域可以看成实Banach空间。因此本书将在Banach空间的框架下给出定义。
设
f
为时标
 到Banach空间
X
上的函数
到Banach空间
X
上的函数
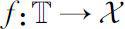 ,对于给定的
,对于给定的
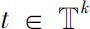 ,若存在
,若存在
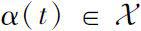 ,对任意给定的
,对任意给定的
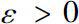 ,存在
t
的
δ
-邻域
,存在
t
的
δ
-邻域
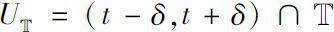 ,使得对任意
,使得对任意
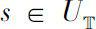 ,都有
,都有

则称
α
(
t
)为函数
f
在点
t
的Δ导数,记为
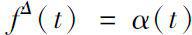 。若
f
在任意的
。若
f
在任意的
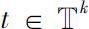 处都存在Δ导数,则称
f
在
处都存在Δ导数,则称
f
在
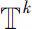 上Δ可微。称为
上Δ可微。称为
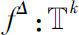 →
X
为
f
在
→
X
为
f
在
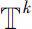 上的Δ导函数。
上的Δ导函数。
当
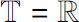 时,Δ导数即为通常的导数;当
时,Δ导数即为通常的导数;当
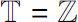 时,Δ导数即为通常的向前差分。因此,时标动力学方程是微分方程与差分方程的统一与推广。2002年,Atici和Guseinov
[9]
将(1.1.1)中的前跃算子
σ
换成后跃算子
ρ
,得到了▽导数的定义。2003年,Anderson和Bullock
[7]
等研究了时标上的▽动力学方程。
时,Δ导数即为通常的向前差分。因此,时标动力学方程是微分方程与差分方程的统一与推广。2002年,Atici和Guseinov
[9]
将(1.1.1)中的前跃算子
σ
换成后跃算子
ρ
,得到了▽导数的定义。2003年,Anderson和Bullock
[7]
等研究了时标上的▽动力学方程。
称函数
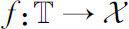 在
在
 上右稠(或左稠)连续,如果
f
在
上右稠(或左稠)连续,如果
f
在
 的右稠(或左稠)点处连续,左稠(或右稠)点处存在有限的左(或右)极限。称函数
的右稠(或左稠)点处连续,左稠(或右稠)点处存在有限的左(或右)极限。称函数
 是
μ
-回归的(或
ν
-回归的),若对任意
是
μ
-回归的(或
ν
-回归的),若对任意
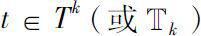 ,都有算子
,都有算子
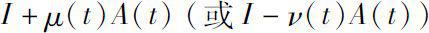 在
B
(
X
)中可逆。将
在
B
(
X
)中可逆。将
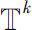 (或
(或
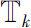 )到
B
(
X
)上全体
μ
-回归(或
ν
-回归)并且右稠连续(或左稠连续)的函数记为
)到
B
(
X
)上全体
μ
-回归(或
ν
-回归)并且右稠连续(或左稠连续)的函数记为
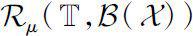 (或
(或
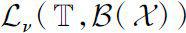 )。
)。
若函数
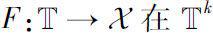 在
在
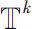 上Δ可微,且对任意
上Δ可微,且对任意
 的,都有
的,都有
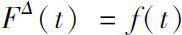 ,则称函数
F
是函数
f
的原函数。进一步,对任意的
,则称函数
F
是函数
f
的原函数。进一步,对任意的
 ,有
f
的Δ-Cauchy积分为
,有
f
的Δ-Cauchy积分为
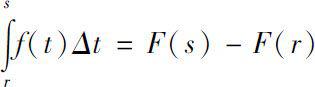 [
11
,
52
,
23
]
。继Cauchy积分之后,人们试图将经典分析学中的各种积分理论推广到时标上来,并讨论了各类积分的性质。如时标上的Riemann积分
[
47
,
46
,
48
]
、Riemann-Stieltjes积分
[89]
、广义积分
[16]
、Lebesgue积分
[
26
,
29
]
及Lebesgue-Stieltjes积分等
[
18
,
20
,
36
]
。
[
11
,
52
,
23
]
。继Cauchy积分之后,人们试图将经典分析学中的各种积分理论推广到时标上来,并讨论了各类积分的性质。如时标上的Riemann积分
[
47
,
46
,
48
]
、Riemann-Stieltjes积分
[89]
、广义积分
[16]
、Lebesgue积分
[
26
,
29
]
及Lebesgue-Stieltjes积分等
[
18
,
20
,
36
]
。
时标动力学方程作为一个热点领域,近些年来受到了国内外许多学者的关注。在解的存在唯一性 [ 23 , 32 , 26 , 30 , 90 , 97 ] 、稳定性 [ 23 , 64 , 56 , 87 , 79 , 58 , 38 , 31 ] 、振动性 [ 42 , 43 , 70 ] 以及周期性 [ 27 , 28 , 98 , 93 ] 等方面取得了丰硕的成果。
其中由Bohner和Peterson在2001年出版的专著《Dynamic equations on time scales: An introduction with applications》中,系统地介绍了时标的基本理论及线性时标动力学方程的相关结果;在2003年出版的专著《Advances in dynamic equations on time scales》中,对文献 [23] 进行了补充,介绍了时标上的▽动力学方程,积分理论及边值问题等方面的研究成果。
现有关于时标动力学方程的研究结果中,多数研究对象为纯量方程或低维向量方程。抽象(包括高维)空间中的动力学方程更具有一般性,因此具有一定的研究价值。本书将研究抽象空间中时标动力学方程的初值问题。