2.2　与 ω 相伴的动态解

由2.1节可知，时标上的线性矩阵方程（1.4.1）的解具有多项式表达，且其系数完全由与 ω 相伴的动态解决定。本节将与 ω 相伴的动态解记为 f _ω （ t ），并讨论 f _ω （ t ）的显式表达。

本节假设 ω （ t ）具有如下形式

其中 a _j 为互不相同的复数， m _j 为非负整数且满足 n ＋1。

由于 ，我们首先考虑微分算子（ D － al ） k 。

如（1.4.6）所示，通过简单演算易得

满足

我们知道，函数集合 时是线性无关的 ^［92］ 。事实上，对于一般的时标 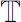，也是线性无关的。

引理2.2.1 设 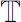为一时标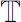， 上的基本广义指数多项式为

则函数集合 线性无关。

证明： 首先证明对于固定的 ，集合 线性无关。

任取 n 个不同的函数

不妨设 k ₁ ＜ k ₂ ＜…＜ k _n 。

若

用 作用（2.2.4）得

故 λ _n ＝0。以此类推可得

即 线性无关。

其次证明函数集合 线性无关。

任取两两不同的 n （ n ＞1）个数 ，设

用算子 作用（2.2.7）有

故有 λ _n ＝0。同理可以证明 λ ₁ ＝ λ ₂ ＝… λ _{n -1} ＝0，所以函数族 线性无关。

下面用数学归纳法证明函数集合 线性无关。

任取两个函数 。

设

若 a ＝ b ，不妨设 k ＜ m ．用 作用（2.2.10）式两端有 ，故 λ ₂ ＝0。再由（2.2.10）式得 λ ₁ ＝0。

若 a≠b ，用 作用（2.2.10）式两端有

故 λ ₂ ＝0。再由（2.2.10）式得 λ ₁ ＝0。

所以 g _a，k ， g _b，m 线性无关。

假设集合 G 中任意 n 个函数线性无关。

任取 n ＋1个两两互不相同的函数 。

设

若 ，用算子 作用（2.2.11）式两端有

从而 λ _{n ＋1} ＝0，由归纳假设得 λ ₁ ＝ λ ₂ ＝…＝ λ _n ＝0。

若 中至少有两个数相等，不妨设 a ₁ ＝ a ₂ ＝… a _m ，且 k ₁ ＜ k ₂ ，…＜ k _m ，其中1＜ m ≤ n ＋1。

用算子 作用（2.2.11）式两端有

从而 λ _m ＝0，再由归纳假设有 。

综上，函数集合 线性无关。

我们把由集合 生成的复向量空间记为 ε ，称 ε 中的元素为广义指数多项式。

易见，函数组 的任意线性组合都是（ D － aI ） ^j 核空间中的元素。因此若 ω 如（2.2.1）所示，则集合 生成的向量空间包含在 ω （ D ）的核空间内。

在集合 S 上定义可交换的卷积运算*。

若 a ≠ b ，定义

其中

若 a ＝ b ，定义

定义线性运算为

对 。

则卷积运算可线性扩张到空间 ε 上。

定义 ε 上的线性泛函Φ为

事实上，即为 处的值。

引理2.2.2 设Φ为 ε 上的线性泛函（2.2.17）。那么对任意 f ，有

证明： 只需验证

再由线性条件即得（2.2.18）。

（2.2.19）式的左端为

（2.2.19）式的右端为

两端 g _b，j ，0≤ j ≤ m 的系数均相等，故（2.2.19）式成立。

与 ω 相伴的动态解 f _ω 可以写成指数多项式的卷积形式，即

下面给出定理1.4.2的证明。

定理1.4.2的证明 ：由卷积的定义易知由 S 生成的 ε 的子空间关于卷积运算*是封闭的，因此 ω （ D ） f _ω ＝0。只需验证 f _ω 满足（1.4.3）的初值条件即可。由（1.2.14）及（2.2.15），我们有

由（2.2.16）知

因此，任意两个指数多项式的卷积在 t ＝0点的值均为零。从而有

下面我们来确定 f _ω 的初值。

若 ω 只有一个 n ＋1重根 a ，则 。令0≤ k ≤ n ，由于 ，有

从而有

若 ω 至少有两个不同的根，设 n ＞1，0≤ k ≤ n 。

f _ω 以写成

其中

由引理2.2.2有 ，故

按（2.2.28）依次迭代得

往证

对 n 用数学归纳法证明（2.2.30）。

当 n ＝1时， 。若 k ＝0，则

若 k ＝1，则

由（2.2.31）及（2.2.32）得 。

假设（2.2.30）在 n 时成立。对 n ＋1，设

其中

由（2.2.2）得 。故

对0≤ k ≤ n ＋1，由（2.2.29）式及（2.2.30）式有

综上，（2.2.30）式成立，故 是与ω相伴的动态解。

我们还可以考虑线性常矩阵▽动力学方程 ^［7］

其中 A 为 m 阶常矩阵， 为矩阵值函数。

称方程（2.2.34）的解为▽矩阵指数函数，记为 。

与Δ动力学方程（1.4.1）的讨论类似，我们可以对应得到▽动力学方程（2.2.34）的求解方法。这里只列出一些主要的内容。

设ω同（1.4.2）。称初值问题

的解为与ω相伴的▽动态解，其中 D 代表▽导算子。

定义时标 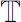上的▽多项式序列为

其中 是方程

的解。

定义时标 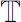上的基本▽指数多项式为

定义卷积运算 为

其中

我们可以利用与ω相伴的▽动态解将矩阵方程（2.2.34）的解表示成 A 的多项式。

定理2.2.1 设 为ω的Horner多项式； 是与ω相伴的▽动态解。

则▽动力学方程（2.2.34）的解（即▽矩阵指数函数）为

证明： 与定理1.4.1类似，略。

由（2.2.41）和（2.2.42）可见，▽矩阵指数函数的系数完全由与ω相伴的▽动态解决定。

我们同样可以得到与ω相伴▽动态解的显式表达式。

定理2.2.2 设ω同（1.4.2），令

则 是与ω相伴的▽动态解。

证明： 证明与定理1.4.2类似，略。

由定理2.2.1和定理2.2.2即可得到▽动态方程（2.2.34）的解的显式表达。

XlFQ3jyecK7IdvNF9a716obrxrxTiYX9X/scBaz0Jwbnerua/8tDSjR5IOmUV5Ku