2.1　线性矩阵动力学方程的解

本节首先介绍时标上广义指数函数的Taylor展式 ^{［ 34 ， 22 ， 21 ］} ，然后给出时标上常矩阵线性动力学方程解的多项式表达，我们将多项式的系数转化为求解时标上的纯量动力学方程。

首先介绍时标上的单项式 ^［3］ 。设 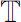为一时标，定义时标 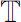上的广义单项式 为

其中 表示固定 s 对变量 t 求Δ导。

由（2.1.1）式知

当 k ＞1时，对一般的时标， φ _k 并不易求得。

当 时，我们有

当 时，我们有

当 时， φ _k 的表达式见文献［ 21 ］。

Bohner和Lutz ^［22］ 对函数 φ _k 作出如下估计。

引理2.1.1 ^［22］ 对任意的 及任意的 ，有

记 处无穷次Δ可微（即 f 在 α 处有任意阶Δ导数），我们可以定义 f 在点 α 处的形式Taylor级数

当 α 和 t 给定时，Taylor级数（2.1.8）收敛的充要条件为

中的余项 。

我们首先介绍Δ指数函数的Taylor展式。

引理2.1.2 ^［22］ 设 ，则初值问题

的唯一解具有Taylor展式

且有不等式

由引理2.1.2知，Δ指数函数 e _p （ t ， s ）的Taylor展式为

类似于引理2.1.2，广义矩阵指数函数 e _A （ t ，0）也可写成Taylor展式。

引理2.1.3 ^［34］ 方程（1.4.1）的唯一解 e _A （ t ，0）在任意区间 上具有Taylor展式

且当 t ≥0时，有不等式

成立。

以上介绍的Taylor展式为 e _A （ t ，0）的无穷级数形式。为方便应用，我们将考虑 e _A （ t ，0）的有限级数形式。由Cayley-Hamilton定理 ^［57］ 知，矩阵 A 的特征多项式 ω （ t ）＝ det （ tl － A ）满足（1.4.2）的要求。

下面介绍方程（1.4.3）解的存在唯一性定理 ^{［ 23 ， 2 ］} 。

引理2.1.4 ^［34］ 设 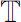为一时标， ω 满足（1.4.2）。如果

那么与 ω 相伴的动力学方程（1.4.3）存在唯一解。

若不加说明，本书总假设动力学方程 （1.4.3）存在唯一解。

引理2.1.5 设 ω 满足（1.4.2），如果 f ₀ 是与 ω 相伴的动态解，那么，方程（1.4.1）的解，即广义矩阵指数函数有以下多项式表达

其中

证明： 由（2.1.16）式得

再由（1.4.2）式得

由（2.1.17）及（2.1.18）式得

由 ω （ A ）＝0有

将（2.1.19）及（2.1.20）联立并整理得

由（1.4.3）的初值条件及（2.1.16）知 满足方程（1.4.1）。

引理2.1.5得到了方程（1.4.1）解的一种显式表达。只需求得与 ω 相伴的动态解 f ₀ （ t ），然后代入（2.1.16）进而带入（2.1.15）即可得到方程（1.4.1）的解。关于动态解 f ₀ （ t ）的具体求法将在下一节介绍。

我们还可以通过另一种方法得到方程（1.4.1）解的显式表达。设 ω （ t ）满足（1.4.2）。定义差商

易知 ω ［ t ， x ］关于变量 t 和 x 是对称的，且有

由多项式恒等式

得

其中

设 X （ t ）为 m 阶矩阵值函数， A 为 m 阶常矩阵。令算子 A 作用在 X （ t ）上为用 A 左乘 X （ t ）；算子 D 作用在 X （ t ）上即为对 X （ t ）的每个位置求Δ导。故算子 D 与 A 可交换。将 ω ［ t ， x ］中的 t 与 x 分别换成算子 D 与 A ，我们可以得到一个常矩阵系数的线性Δ微分算子 ω ［ D ，A］。由（2.1.23）有

利用（2.1.27）可以得到方程（1.4.1）的解，即广义矩阵指数函数的多项式形式（见定理1.4.1）。

定理1.4.1的证明 ：用（2.1.27）两端同时作用在矩阵值函数 f （ t ） I （其中 I 是单位阵）上得

即矩阵值函数 。

由（2.1.25）有

再由 f （ t ）的初值条件（1.4.3）可得 X （0）＝ I 。

易见定理1.4.1中的（1.4.4）式与定理2.1.5中的（2.1.15）式相同。

I9y6ODbdR+qk/RHKPWyX2SM3ynHQfXrip0PFWpEIpVwsJupGCR1zCkNiHKNVkUih