




函数极限的ε-δ(或ε-X)定义以及上一节的定理2,都只能用来验证数A是否为函数的极限.不仅验证过程较为繁复,而且若事先无法确定数A,就没办法操作了.为此,我们有必要发展一套直接计算极限的方法与规则.在以下的讨论中,引进记号“lim”,它泛指自变量的各种变化过程,也即不管是x→x 0 ,或是x→∞,还是单侧极限,法则都是适用的.不过证明时,我们只对x→x 0 给出.
函数极限也有与数列极限类似的四则运算法则,其前提条件是各有关函数的极限都是存在的.
定理1 若极限limf(x)=A,limg(x)=B,则
(1)lim[f(x)±g(x)]=limf(x)±limg(x)=A±B;
(2)lim[f(x)g(x)]=limf(x)·limg(x)=AB;
(3)
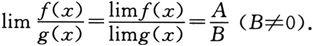
证 仅证(2),另外两个结论的证明留给读者.
因limf(x)=A,limg(x)=B,由§1.4的定理2,应有f(x)=A+α,g(x)=B+β,其中α和β都是同一变化过程的无穷小,所以
f(x)g(x)-AB=(A+α)(B+β)-AB=Aα+Bβ+αβ.
由无穷小的运算性质知,Aα,Bβ和αβ都是无穷小,从而其和也是无穷小.因此,再由§1.4的定理2得
lim[f(x)g(x)]=AB=limf(x)·limg(x).
注 定理1的(1)和(2)均可推广到有限个函数的情形.
推论 若极限limf(x)=A,则
(1) lim[Cf(x)]=Climf(x)=CA,其中C为常数;
(2)lim[f(x)] n =[limf(x)] n =A n ,其中n是正整数.
下面举几个例子说明极限四则运算法则的应用.
例1 求极限
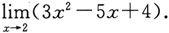
解
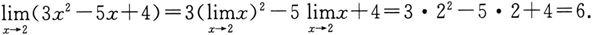
若记f(x)=3x 2 -5x+4,从上面计算过程可以看出
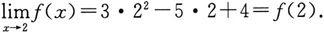
推广 例1的结论可以推广到一般的有理整函数(多项式)的极限:设多项式
P(x)=a 0 x n +a 1 x n-1 +…+a n ,
则
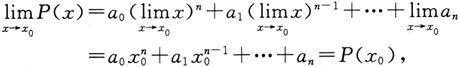
即多项式P(x)当x→x 0 时的极限等于P(x)在x 0 处的函数值P(x 0 ).
例2 求极限
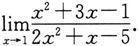
解 根据例1的推广,可得
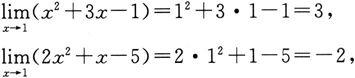
所以
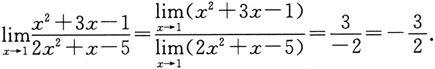
推广 对于一般的有理分式函数
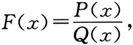 其中P(x),Q(x)都是多项式,根据例1的推广,有
其中P(x),Q(x)都是多项式,根据例1的推广,有
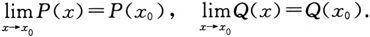
设Q(x 0 )≠0,则
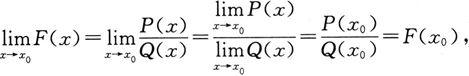
即有理分式函数
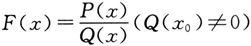 当x→x
0
时的极限等于F(x)在x
0
处的函数值F(x
0
).
当x→x
0
时的极限等于F(x)在x
0
处的函数值F(x
0
).
值得注意的是,若Q(x 0 )=0,则关于商的极限运算法则不再适用,因而上述推广的结论就不成立.
例3 求极限
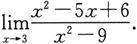
解 因分母极限为0,所以商的极限运算法则不能用.注意到分子的极限也为0,可采用因式分解的方法加以化简:
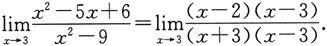
由于x→3是x≠3而趋于3,因而
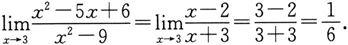
注 当分子、分母的极限均为0时,这种分式的极限称为
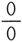 型未定式.之所以称为“未定式”,是因为这类分式的极限可能存在,也可能不存在,不能一概而论,它存在与否取决于分式的具体形式,需具体问题具体分析.最常用的方法是把分子、分母因式分解,约去极限为0的因子,化为分母极限不为0的商的极限,再运用极限运算法则.
型未定式.之所以称为“未定式”,是因为这类分式的极限可能存在,也可能不存在,不能一概而论,它存在与否取决于分式的具体形式,需具体问题具体分析.最常用的方法是把分子、分母因式分解,约去极限为0的因子,化为分母极限不为0的商的极限,再运用极限运算法则.
极限的未定式一共有七种类型:
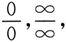 0·∞,∞-∞,1
∞
,∞
0
,0
0
,今后会陆续遇到.求未定式的极限,是极限计算重点关注的问题.
0·∞,∞-∞,1
∞
,∞
0
,0
0
,今后会陆续遇到.求未定式的极限,是极限计算重点关注的问题.
例4 求极限
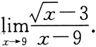
解 当x→9时,分子、分母的极限均为0,它是
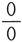 型未定式.先进行因式分解,再利用极限运算法则,得
型未定式.先进行因式分解,再利用极限运算法则,得
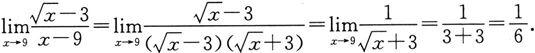
例5 求极限
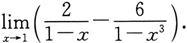
解 当x→1时,
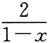 和
和
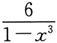 均为无穷大,这是∞-∞型未定式,也不能直接使用极限运算法则.对它可先通分,化为分式极限,再进行计算:
均为无穷大,这是∞-∞型未定式,也不能直接使用极限运算法则.对它可先通分,化为分式极限,再进行计算:
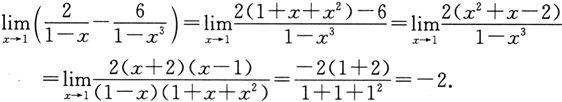
例6 求下列极限:
(1)
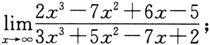
(2)
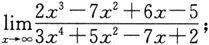
(3)
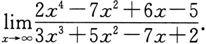
解 (1)显然,当x→∞时,分子、分母都是无穷大,这是
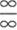 型未定式.分子、分母同除以x的最高次数x
3
,再求极限:
型未定式.分子、分母同除以x的最高次数x
3
,再求极限:
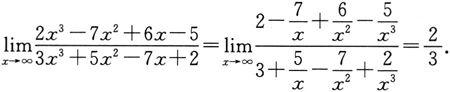
(2)这也是
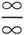 型未定式,且分母的次数比分子的次数高.先分子、分母同除以x的最高次数x
4
,再求极限,得
型未定式,且分母的次数比分子的次数高.先分子、分母同除以x的最高次数x
4
,再求极限,得
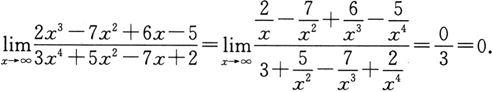
(3)此时分子的次数比分母的次数高,先考虑分子、分母对调的分式的极限:
可见,当x→∞时,
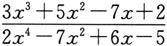 是无穷小,从而
是无穷小,从而
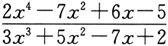 为无穷大,也即
为无穷大,也即
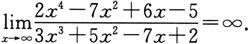
从例6的三个小题可以看出,当x→∞时,有理分式函数的极限是
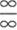 型未定式,它取决于分子、分母关于变量x的次数.若分子、分母关于变量x的次数相等,则其极限等于分子、分母最高次数项的系数之比;若分母的次数比分子高,则其极限为0;若分子的次数比分母高,则其极限为∞.用数学式表达如下:
型未定式,它取决于分子、分母关于变量x的次数.若分子、分母关于变量x的次数相等,则其极限等于分子、分母最高次数项的系数之比;若分母的次数比分子高,则其极限为0;若分子的次数比分母高,则其极限为∞.用数学式表达如下:
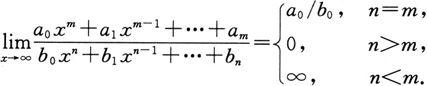
显然,分子、分母中的低次项不起作用,关键看的是它们的最高项.因此,可以形象地把计算过程概括为“抓大放小”,只需求最高项比的极限就够了.例如:
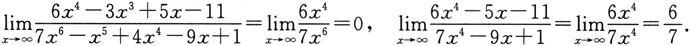
极限的四则运算法则大大拓宽了极限计算的范围,我们摆脱了步步依靠极限的ε-δ(或ε-X)定义来验证极限(而非求极限)的困境.但是,仍然有很多简单的问题没办法直接求解.例如,对于极限
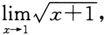 尽管前面已经知道
尽管前面已经知道
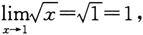 但缺少依据来说明
但缺少依据来说明
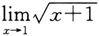
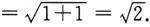 不难发现,
不难发现,
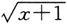 是由
是由
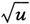 与u=x+1复合而成的.因此,有必要研究复合函数的极限问题.对此,我们有如下的结论:
与u=x+1复合而成的.因此,有必要研究复合函数的极限问题.对此,我们有如下的结论:
定理2(复合函数的极限运算法则) 设函数y=f(φ(x))是由函数y=f(u)与函数u=φ(x)复合而成的,f(φ(x))在点x
0
的某个去心邻域内有定义.若极限
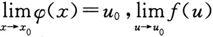
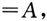 且存在δ
0
>0,当0<|x-x
0
|<δ
0
时,有φ(x)≠u
0
,则
且存在δ
0
>0,当0<|x-x
0
|<δ
0
时,有φ(x)≠u
0
,则
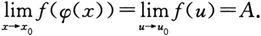
证明略.
上述定理说明,在定理条件下求极限
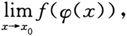 可以通过作代换u=φ(x),把所求极限转化为
可以通过作代换u=φ(x),把所求极限转化为
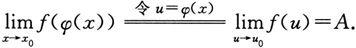
将极限过程x→x
0
换为x→∞,或者把
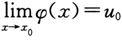 换为
换为
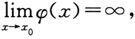 同时把
同时把
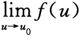 =A换为
=A换为
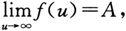 可以得到类似的结论.
可以得到类似的结论.
例7 求极限
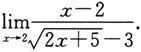
解 作代换u=2x+5,则
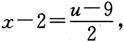 且当x→2时,有u→9.由定理2得
且当x→2时,有u→9.由定理2得
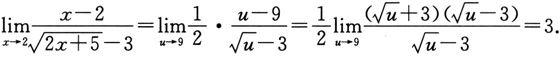
若作代换
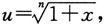 我们容易证明:
我们容易证明:
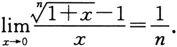
这个结论可以作为公式直接应用.
例8 求极限
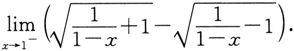
解 作代换
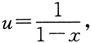 则当x→1
-
时,u→+∞.由定理2得
则当x→1
-
时,u→+∞.由定理2得

例9 求极限
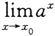 (a>0且a≠1).
(a>0且a≠1).
解 由对数恒等式N=e
lnN
得a
x
=e
xlna
.于是a
x
是由f(u)=e
u
与u=φ(x)=xlna复合而成的复合函数.由于
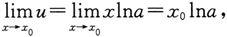 由定理2知
由定理2知
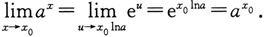
在§1.1例5中我们知道,幂指函数u(x) v(x) (u(x)>0与v(x)是初等函数)仍然是初等函数.如何求x→x 0 时幂指函数的极限呢?仿照例9,应用对数恒等式与复合函数的极限运算法则,易得下面的推论:
推论(幂指函数的极限) 设u(x)>0 与v(x)是初等函数,且极限
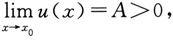
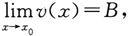 则有
则有
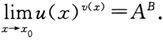
1.求下列极限:
(1)
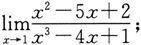
(2)
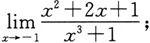
(3)
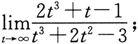
(4)
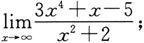
(5)
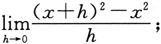
(6)
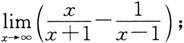
(7)
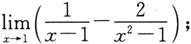
(8)
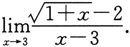
2.求下列极限:
(1)
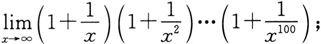
(2)
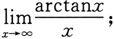
(3)
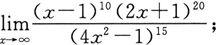
(4)
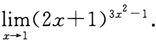
3.设函数
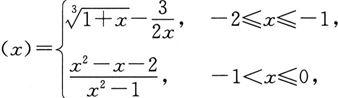 求极限
求极限
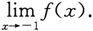
4.若极限
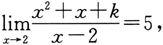 求常数k的值.
求常数k的值.