




这一节我们要研究两类特殊的量:一类是以零为极限的量;另一类量虽说在其变化过程中极限不存在,但其绝对值无限增大,是特殊的发散的量.这两类量在数列与函数极限的研究中起着十分重要的作用,它们就是下面要介绍的无穷小量与无穷大量.
定义1 以零为极限的量称为无穷小量,简称为无穷小.具体地说,若当x→x
0
(或x→∞)时,f(x)→0,则称函数f(x)为当x→x
0
(或x→∞)时的无穷小.特别地,若
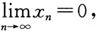 ,则称数列{x
n
}为无穷小.
,则称数列{x
n
}为无穷小.
例如,f(x)=2x是当x→0时的无穷小;数列
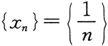 是无穷小,
是无穷小,
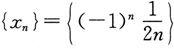 也是无穷小.
也是无穷小.
注 无穷小是一个量,是一个在其自变量的变化过程中,绝对值变得可以小于任意事先给定的正数的量.因此,除了常数0外,任何的非零常数都不可能是无穷小.
定义2 若对于任意给定的正数M(不管它多么大),总存在正数δ(或正数X),使得当0<|x-x 0 |<δ(或|x|>X)时,恒有
|f(x)|>M,
则称函数f(x)为当x→x 0 (或x→∞)时的无穷大,记为
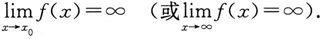
类似地,可以定义
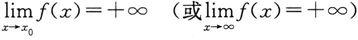
与
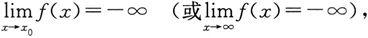
此时只需把定义2中的|f(x)|>M分别改为f(x)>M与f(x)<-M即可.
注1 无穷大是一个量而不是一个数,任何很大的数都不是无穷大.
注2
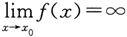 只是一个记号,并不代表函数f(x)的极限存在.相反地,此时函数极限不存在,它是函数极限不存在的一种特殊形式.
只是一个记号,并不代表函数f(x)的极限存在.相反地,此时函数极限不存在,它是函数极限不存在的一种特殊形式.
注3 一个函数是否为无穷大或无穷小,与自变量的变化过程息息相关.例如,函数
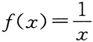 当x→0时是无穷大,而当x→∞时却是无穷小;当x→x
0
(x
0
≠0为有限数)时,
当x→0时是无穷大,而当x→∞时却是无穷小;当x→x
0
(x
0
≠0为有限数)时,
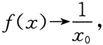 从而此时f(x)既不是无穷小,也不是无穷大.
从而此时f(x)既不是无穷小,也不是无穷大.
注4 我们不加证明地给出如下事实:
(1)与§1.3单侧极限的定理1平行,有
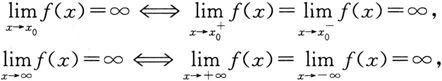
其中⇔表示等价.
(2)
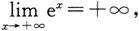 而
而
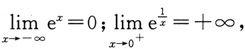 而
而
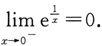
若以a>1代替e,上述(2)中的公式仍成立.
上述几个极限公式十分常用,必须牢记.
由定义可以看出,无穷小与无穷大之间存在着天然的联系.
定理1 在自变量x的同一变化过程中,若f(x)为无穷大,则
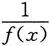 为无穷小;反之,若f(x)为无穷小,且f(x)≠0,则
为无穷小;反之,若f(x)为无穷小,且f(x)≠0,则
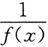 为无穷大.
为无穷大.
证 仅对x→x 0 的情形加以证明.
设
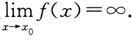 对于任意事先给定的正数ε,取
对于任意事先给定的正数ε,取
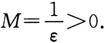 按定义,存在δ>0,当0<|x-x
0
|<δ时,恒有
按定义,存在δ>0,当0<|x-x
0
|<δ时,恒有
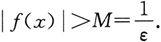 由此得
由此得
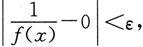
这说明,当x→x
0
时,
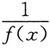 为无穷小.
为无穷小.
反之,设
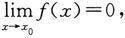 且f(x)≠0.对于任给的正数M,取
且f(x)≠0.对于任给的正数M,取
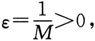 按定义,存在δ>0,当0<|x-x
0
|<δ时,恒有
按定义,存在δ>0,当0<|x-x
0
|<δ时,恒有
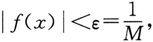 从而
从而
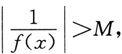
所以
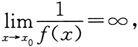 也即当x→x
0
时,
也即当x→x
0
时,
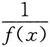 为无穷大.
为无穷大.
在上述注4中,只需令t=-x,再应用定理1,读者很容易由
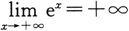 自行推导出另一个极限
自行推导出另一个极限
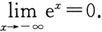
用极限的ε-δ(或ε-X)定义去验证数A是否为函数的极限,相对来说是比较复杂的.有了无穷小概念,我们可以建立函数极限存在的一个等价性定理,通过它把函数极限的问题转化为常数与无穷小的代数运算问题,从而在验证极限,尤其是在理论上证明和推导极限方面带来便利.
定理2 极限
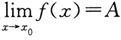 的充分必要条件是f(x)=A+α,其中α是当x→x
0
时的无穷小.
的充分必要条件是f(x)=A+α,其中α是当x→x
0
时的无穷小.
证 必要性 设
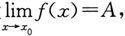 则对任意给定的正数ε,存在正数δ,使得当0<|x-x
0
|<δ时,恒有
则对任意给定的正数ε,存在正数δ,使得当0<|x-x
0
|<δ时,恒有
|f(x)-A|<ε,
令α=f(x)-A,则f(x)=A+α,且
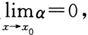 也即α是当x→x
0
时的无穷小.
也即α是当x→x
0
时的无穷小.
充分性 设f(x)=A+α,其中α是当x→x 0 时的无穷小,则有
α=f(x)-A,
并且由无穷小的定义知,对任意给定的正数ε,存在正数δ,使当0<|x-x 0 |<δ时,恒有
|α|<ε,也即|f(x)-A|<ε,
由此得
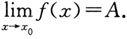
注 定理2对于自变量的其他变化过程仍然成立.
由定理2可以看出,在极限的验证与计算中,无穷小的代数运算是重要的.下面不加证明地介绍无穷小的运算性质,证明过程请读者自行补出.
定理3 有限个无穷小的代数和仍为无穷小.
定理4 有限个无穷小的积仍为无穷小.
定理5 有界函数与无穷小的乘积仍为无穷小.
推论 常数与无穷小的乘积仍为无穷小.
例 求极限
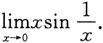
解 因为
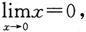 即当x→0时,x是无穷小,而
即当x→0时,x是无穷小,而
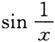 是有界函数,由定理5知
是有界函数,由定理5知
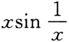 也是无穷小,因此
也是无穷小,因此
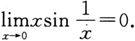
类似地,可以证得
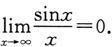
注 从有限到无限,是量变到质变的过程.有限个无穷小的代数和仍为无穷小,而无穷多个无穷小的和就未必是无穷小,这一点应引起注意.例如,
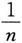 当n→∞时是无穷小,有限个(比如k个,k是有限数)
当n→∞时是无穷小,有限个(比如k个,k是有限数)
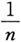 相加等于
相加等于
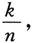 仍为无穷小.但是,n个
仍为无穷小.但是,n个
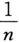 的和却等于常数1,它当n→∞时不再是无穷小.若n
2
个
的和却等于常数1,它当n→∞时不再是无穷小.若n
2
个
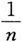 相加,其和为n,当n→∞时却变为无穷大.类似地,无穷多个无穷小的乘积也未必是无穷小.
相加,其和为n,当n→∞时却变为无穷大.类似地,无穷多个无穷小的乘积也未必是无穷小.
1.判断题:
(1)x 2 是无穷小; ( )
(2)零是无穷小; ( )
(3)无穷多个无穷小的和仍然是无穷小; ( )
(4)两个无穷小的商是无穷小; ( )
(5)两个无穷大之和一定是无穷大; ( )
(6)无穷大必为无界函数; ( )
(7)有界函数与无穷小的乘积仍然是无穷小; ( )
(8)有界函数与无穷大的乘积仍然是无穷大. ( )
2.指出下列哪些是无穷小量,哪些是无穷大量:
(1)
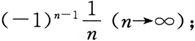
(2)
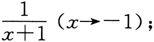
(3)
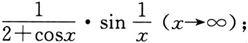
(4)
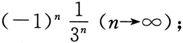
(5)

3.设当x→x 0 时,α(x)为无穷小,β(x)为无穷大,则( )必为无穷大.
(A)α(x)+β(x)
(B)
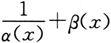
(C)α(x)β(x)
(D)
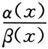
4.当x→∞时,函数f(x)=xsinx是( ).
(A)无穷小
(B)无穷大
(C)有界函数
(D)无界函数
5.根据定义证明函数
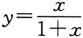 为当x→0时的无穷小.
为当x→0时的无穷小.