1.3　命题公式与真值函数

通过前面两节的讨论，已经引入了5个逻辑联词，得到了5个最简单的复合命题形式，从这些复合命题形式出发，由逻辑联词再经过各种相互组合，可以构成更多、更复杂的复合命题形式。这些命题形式一般称命题公式，那么怎样的组合形式才是命题逻辑的命题公式呢？

命题逻辑的命题公式是一个含有命题常元、命题变元及逻辑联词和圆括号的表达式，并以下述规则递归定义：

（1）基础：命题变元是命题公式；

（2）归纳：若A是命题公式，则（﹁A）也是命题公式；

若A，B是命题公式，则（A∨B），（A∧B），（A→B）和（A↔B）也都是命题公式；

（3）界限：当且仅当由（1）、（2）的有限次应用生成命题逻辑的全部命题公式。

为了简化圆括号的使用且不至引起表达的混淆，约定如下规则：

（1）合式公式的最外层括号可以略去；

（2）规定逻辑联词的运算先后次序为：﹁，∨，∧，→，↔。

【例1.3.1】　设P，Q为命题变元，按照命题公式的递归定义，可知P，（﹁Q），（P∧﹁Q），（﹁Q∨P），（（P→﹁Q）↔﹁Q），﹁（P∧﹁Q）∨（（﹁P∨﹁﹁Q）∧（﹁Q∨P））→（﹁（P↔﹁Q）∧（﹁P→﹁Q））都是命题公式。再由圆括号省略和逻辑联词的优先次序的约定，上述命题公式可以写为：P，﹁Q，P∧﹁Q，﹁Q∨P，P→﹁Q↔﹁Q，﹁（P∧﹁Q）∨（﹁P∨﹁﹁Q∧﹁Q∨P）→﹁（P↔﹁Q）∧﹁（﹁P→﹁Q）。

需要注意：圆括号的使用仅仅是对运算施行先后的区分，只要能够严格表述运算的次序，圆括号省略、少省略、不省略都是允许的。

将由自然语言表述的命题写成符号形式，就是要将由自然语言叙述的命题写成由原子命题符号、逻辑联词符号及圆括号表示的与其等值的命题框架，即将命题符号化或翻译为命题公式，这是一个困难而复杂的问题。一般只要求对一些常见的逻辑结构较为清晰的命题语句能做出正确的翻译。

为了翻译准确，需要客观地分析与理解自然语言命题，认真确定语句中的原子陈述句和语句中的连接词是怎样的逻辑联词，进而采用“真值表方法”进行取值对照，通过真值表上真值对照，容易检查公式翻译是否妥贴，而且还能克服情感、心态等方面的干扰或影响。

【例1.3.2】　（1）考虑对命题“只有你走我才留下”的翻译。

这一命题是说：“若你不走，则我不留”；也是说：“如若我留则你得走”。因此，它的正确翻译是：

令P为“你走”，Q为“我留”，则原命题的真值形式是：﹁P→﹁Q，亦即：Q→P。

与原命题类似的命题还有：

仅当你走我才留下；

仅当你走我将留下；

我留下仅当你走。

在一般的命题表述中，“仅当”是必要条件，译成条件命题时其后的命题是后件；而“当”是充分条件，译成条件命题时其后的命题是前件。

（2）考虑对命题“我今天进城，除非下雨”的翻译。

这一命题是说：“若不下雨，则我今天进城”，或者是说：“我今天不进城，仅当要下雨”。因此，它的正确翻译是：

令P为“我今天进城”，Q为“今天下雨”，则原命题可以符号化为﹁Q→P，亦可：﹁P→Q。

“除非”，表示唯一的条件，原命题相当于“只有天下雨我才不进城”。

单用“除非”的命题，“非……”是充分条件，译成条件命题时，“非……”是前件。要是“除非……，否则……”的命题，其真值形式就是双条件了。

（3）考虑对命题“小张或小李都可以办好这件事”的翻译。

令P为“小张可以办好这件事”，Q为“小李可以办好这件事”，则原命题F（P，Q）的真值表见表1-6。

表1-6　原命题的真值表

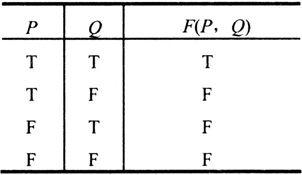
从真值表可得F（P，Q）＝P∧Q。所以要翻译成合取形式，“都”字起了决定性作用。如果原命题中略去“都”字，那么就要翻译成析取形式的命题公式。

在例1.3.2之（3）的讨论中，使用了标记“F（P，Q）”。其含义是：要求的命题形式由原子命题P，Q组成，该命题形式在｛T，F｝上定义，且在｛T，F｝上取值。换句话说，F（P，Q）是函数，F（P，Q）是以｛T，F｝为定义域和值域的真值函数。

事实上，每一命题形式都确定一个函数，这一函数的自变元是命题形式中的命题变元，它的定义域和值域都是真值集｛0，1｝，这样的函数称为真值函数。

当命题变元给定以后，由这些命题变元组成的命题公式是无限多的，但以给定命题变元为自变元的真值函数是有限的。

【例1.3.3】　考虑只含有一个命题变元P的真值函数F（P）。

由于只含有一个命题变元P，F（P）的真值取值只有两种选择。即当P分别取真值T、真值F时F（P）的取值各是什么。把F（P）的取值列成以下真值表（见表1-7）。

F ₃ （P）是一常真的函数，命题形式P∨﹁P，（P∨﹁P）∨X（X表示由命题变元P组成的任一命题公式）等都是这种真值函数；F ₂ （P）取值与P，P∧P，P∧P∧P，…取值一致；F ₁ （P）与﹁P，﹁P∨﹁P，﹁P∨﹁P∨﹁P，…取值相同；F ₀ （P）是一永假的函数，P∧﹁P，（P∧﹁P）∧X就是与它取值完全一样的命题形式。

表1-7　F（P）的取值真值表

由例1.1.3可见，只含有一个命题变元的不同的真值函数有 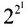个，显然更一般的结论是含有n个命题变元的不同的真值函数有 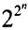个。

当命题变元的数目确定以后，不同的真值函数的数目是有限且确定的，但命题形式的数目却是无限的，它们是分别与相应命题函数取值一致的一组组命题公式。不同的命题形式可以表示相同的函数，从中找出一个形式最简单或具有某种标准形式的命题公式，将是我们感兴趣的问题。

练习1-3

（1）下列字符串是否是命题逻辑的命题公式？

①R∨（Q→P））；

②（（（﹁P→Q）→（Q→P））；

③﹁（P→Q）↔﹁﹁P∧Q→R。

（2）公式的代入与代入实例是指命题公式A（P），将A中命题变元P的每一出现均代换为命题变元B，所得的公式A（B）称为原公式的代入实例。

①考虑下列命题公式组中后一公式是否是前一公式的代入实例：

（（P→Q）→Q）→P，（（（A→C）→（（B∧C）→A））→（（B∧C）→A））→（A→C）（式中A，B，C是任意命题公式）；

P→（Q→P），Q→（（P→P）→Q）；

P→（Q→P），P→（（P→（Q→P））→P）。

②证明“代入原理”：设A（P）为含有命题变元P的永真命题形式，B是任一命题公式，则A（P）的代入实例A（B）仍为永真命题形式。

（3）翻译下列命题为命题公式（句中括号内提示的是相应原子命题的符号表示）：

①或者你没有给我写信（P），或者它在途中丢失了（Q）。

②如果小张（P）和小李（Q）都不去，小王就去（R）。

③如果金是金属（P），那么金能导电（Q），金是金属，故金能导电。

④只有身体好（P），才能学习好（Q）。

⑤只要这本书有用（P），他就买回来（Q），虽然他不富（R）。

⑥他一定能自学毕业（P），除非他旧病复发（Q）。

⑦人不犯我（P），我不犯人（Q）；人若犯我，我必犯人。

⑧不管明天是刮风（P）还是下雨（Q），我们定去郊游（R）。

（4）利用列出不同真值取值的方法，考虑F（P，Q）的个数。对每个真值函数，给出一个与它取值相同的至多含有两个命题变元的命题公式。 JthNt42tf2/nN7puv3bXpLE0kPTO/pQsXrICqjzWc8S8aYEr5YSXaScfoLlPa1v8