




1.否定,﹁
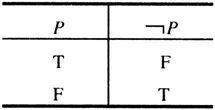
命题P的否定是命题﹁P,读作非P。从真值表易见P与﹁P的取值关系:P真,当且仅当﹁P假(见表1-1)。
表1-1 否定
2.合取,∧
命题P与Q的合取是命题P∧Q,读作P与Q。P∧Q“真”,当且仅当P与Q都真(见表1-2)。
显然P∧﹁P是一永假式。
表1-2 合取
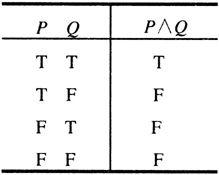
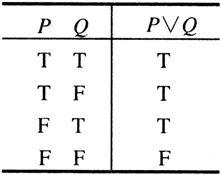
表1-3 析取
3.析取,∨
命题P与Q的析取是命题P∨Q,读作P或Q。P∨Q假,当且仅当P与Q都假(见表1-3)。
易见P∨﹁P是一永真式。
命题P与Q的析取命题P∨Q取真值时,允许P和Q同时取得真值真,即P与Q可同真,因而也说析取∨是可兼或。
4.条件,→
命题P与Q组成条件命题P→Q,读作若P则Q。其中P称前件,Q称后件。P→Q假,当且仅当P真而Q假(见表1-4)。
表1-4 条件
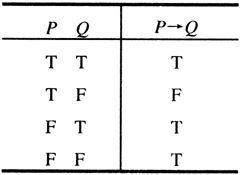
表1-5 双条件
条件命题P→Q当前件P取值为假时,无论后件取值是真还是假,它都为真,即从假的前件出发不管推断的后件是真还是假,P→Q都为真。这一定义方法被理解为“善意的推定”。P→Q在P为假时被规定为真的规定称“实质蕴涵”规定。
5.双条件,↔
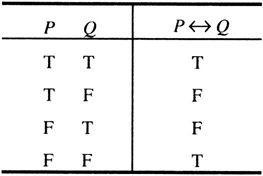
命题P与Q组成双条件命题P↔Q,读作P当且仅当Q。P↔Q取真,当且仅当P与Q取相同的真值即同取真值真或同取真值假(见表1-5)。
这里称P为双条件命题的左支,称Q为右支。
由原子命题通过逻辑联词连接或作用组成最简单的复合命题,逻辑联词对复合命题的作用可以形成更为复杂的命题。命题都有真假,原子命题的真假取决于它是否与客观实际相符合,复合命题的真假由组成它的支命题和逻辑联词的严谨定义所确定。
需要注意的是:逻辑联词与自然语言中相应词语的含义既有联系,又有区别,而且被逻辑联词连接和作用的支命题只要求是具有真假值之一值的命题,而并不强调支命题间是否在内容上都有联系。
逻辑联词反映复合命题与支命题之间的真值关系,它们有确定的含义,不能与自然语言中的相应词语混为一谈。逻辑联词是自然语言中相应词语的抽象。
从逻辑联词的真值取值定义表中可以看出,逻辑联词将{0,1}映射为{0,1}。
练习1-2
(1)指出下列语句中的“并非”、“并且”、“与”、“或者”、“只有……,才……”、“……,仅当……”、“除非……,否则……”等词是否就是我们定义的相应逻辑联词:
①她并非江竹婷。
②小朱拉开抽屉并且取出一本书来。
③东风压倒西风,或者西风压倒东风。
④仅当我去,你不去。
⑤小梁与小孟是好朋友。
⑥除非敌人投降,否则他们没有出路。
⑦整数i只有能被2整除,i才能被4整除。
⑧若天不下雨,则我去书店。
(2)指出下列命题的真值:
①如果2+2=5,那么太阳从西边升起。
②如果太阳不从东边升起,那么地球就停止自转。
③胎生动物当且仅当是哺乳动物。
④若元素a属于空集∅,则属于集合A。
⑤锄禾日当午,汗滴禾下土。
⑥除非ABCD是平行四边形,否则它的对边不都平行。
(3)令P=“天下雪”,Q=“我去镇上”,R=“我有空闲”,请将下列命题符号化:
①如果天下雪且我没有空闲,那么我不去镇上。
②我去镇上当且仅当我有空闲。
③天不下雪。
④除非下雪,否则我去镇上。
⑤或者下雪,或者我有空闲。
⑥天在下雪,我在去镇上。
(4)填空:将逻辑联词或原子命题或其否定填入空挡处。
①
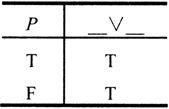
②
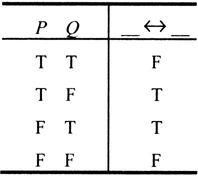
③
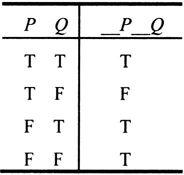
(5)在条件命题中,“善意的推定”是指什么?在析取命题中可兼或的含义是什么?


