下载掌阅APP，畅读海量书库
立即打开
范式是公式的一种标准形式。从等值的意义上讲，一个真值函数，有许多不同形式的命题公式。例如，P↔Q＝（P→Q）∧（Q→P）＝（﹁P∨Q）∧（P∨﹁Q）＝（P∧Q）∨（﹁P∧﹁Q）＝…（见表1-14）。但实际上，它们都是具有下列真值表的同一真值函数。
表1-14 真值表
如果选定形为（P∧Q）∨（﹁P∧﹁Q）或（P∨﹁Q）∧（﹁P∨Q）的命题形式为F 9 （P，Q），那么就说，它们是F 9 （P，Q）的规范形式（所以要在F上加注下标9，是因为将这类公式的真值取值TFFT，作1001看，这个二进制数的十进制值是2 3 ＋2 0 ＝9）。这种规范形式有怎样的标准呢？
说一个命题公式G有合取范式，如果G满足：（1）G＝A 1 ∧A 2 ∧…∧A n （n≥1），（2）每个A i （i＝1，2，…，n）都是G中所含某些命题变元及其否定的析取式；说一个命题公式G有析取范式，如果G满足：（1）G＝B 1 ∨B 2 ∨…∨B m （m≥1），（2）每个B i （i＝1，2，…，m）都是G中所含某些命题变元及其否定的合取式，这样的A i 称简单析取式或子句，B i 称简单合取式或短语。
像（P∨Q∨﹁P）∧（﹁Q∨R）就是一个合取范式，而（P∧Q∧﹁P）∨（﹁Q∧R）则是析取范式。特别一个命题变元P或它的否定﹁P既可以看作一个合取范式，也可以看作一个析取范式；当然既可以看作简单析取式，也可以看作简单合取式。至于P∨Q∨﹁P如果看它为短语的析取，那么它是析取范式，如果看它为子句，那么它是合取范式。
任一命题公式G的合取范式和析取范式总是可以求得的。或者说，任一命题公式G都存在与之等值的合取范式和析取范式。只要首先把G等值归化到｛﹁，∧，∨｝上，而后利用反演律将﹁移至命题变元前（即否定深入），再由重非律、结合律和分配律便可求得所要求取的范式了。在使用分配律时，如果求析取范式，一般要用短语对析取式进行分配；如果求合取范式，则用子句对合取式进行分配。
【例1.8.1】 （P∧﹁（Q→R））∨S
命题变元及其否定称为互否文字。对命题公式G，当其合取范式中每个简单析取式里都至少含有一对互否文字时，则G为重言式；当G的析取范式中每个简单合取式里都至少含有一对互否文字时，则G为矛盾式。通过有限步求出一个命题公式的范式，由范式确定该命题公式是重言式，是矛盾式，还是可满足式的问题被称之为判定问题。所谓判定问题，是指能否给出一个可行方法，对任意命题公式，判定其是否为重言式。因而也能判断出所给公式是否为矛盾式，或一般可满足式。采用求合取范式和析取范式的方法能判定出一个命题公式是否重言式或不可满足式。但一个命题公式的合取范式和析取范式其规范性还不够标准、也不唯一。例如：
（1）设G 1 ＝（P→Q）∧（Q→R）∧（R→P），则（﹁P∨Q）∧（P∨﹁R）∧（﹁Q∨R）和（P∨﹁Q）∧（﹁P∨R）∧（Q∨﹁R）都是G 1 的合取范式；
（2）设G 2 ＝（P→﹁（Q∧R））∧（P∨Q∨R），则（P∧﹁Q）∨（﹁P∧R）∨（Q∧﹁R）和（﹁P∧Q）∨（P∧﹁R）∨（﹁Q∧R）都是G 2 的析取范式；
（3）给G 1 的合取范式合取上含有互否文字的子句，还是G 1 的合取范式；给G 2 的析取范式析取上含有互否文字的短语，还是G 2 的析取范式。
合取范式与析取范式的不唯一性，与选定一种命题形式作为与它真值取值相同的一类命题形式（表示这类命题形式的是一真值函数）的规范形式的初衷尚有距离。下面介绍主范式。主范式与表示一类等值命题公式的真值函数是相互唯一确定的。
n个命题变元的布尔合取或极小项，是形如
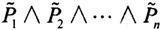
的简单合取式，式中
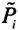要么是P
i
，要么是﹁P
i
（i＝1，2，…，n）。
n个命题变元的布尔析取或极大项，是形如
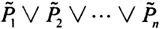
的析取式，式中
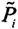要么是P
i
，要么是﹁P
i
（i＝1，2，…，n）。
布尔合取与布尔析取规定n个命题变元中的每一个，按照命题变元的字母顺序依次或者它自己，或者它的否定必须有一且只需有一出现在合取及析取式中。
由极小项构成的析取范式，称主析取范式；由极大项构成的合取范式，称主合取范式。主范式的特殊作用在于它们可以显示出真值函数的一些重要特征。
n个命题变元的极小项共有2
n
个，n个命题变元的极大项也有2
n
个，因为对
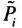，i＝1，2，…，n的这n个位置的每一个上，要么选P
i
，要么选﹁P
i
，都有两种选择，相应于n个位置，就有2
n
种选择。每一种选择，就是一个极小（大）项，所以n个命题变元的不同极小（大）项共有2
n
个。
两个命题变元的全部极小项是：
﹁P∧﹁Q，﹁P∧Q，P∧﹁Q，P∧Q。并分别将它们记为：m 00 ，m 01 ，m 10 ，m 11 。这里m的下标标记的方法是：若对应于小项中出现的是命题变元，则标为1；若出现的是命题变元的否定形式，则标为0。易见，这还是一个二进制表示。二位二进制数有2 2 ＝4个，二位极小项也有2 2 ＝4个，可见二位二进制数与二位极小项一一对应。
3个命题变元的小项有2 3 ＝8个，三位二进制数也有2 3 ＝8个。于是有：
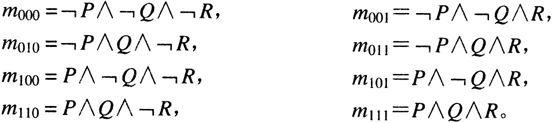
显然，三位二进制数与三位极小项一一对应。
两个命题变元的极大项是：
P∨Q，P∨﹁Q，﹁P∨Q，﹁P∨﹁Q。并分别将它们记为：M 00 ，M 01 ，M 10 ，M 11 。这里下标标记的方法是：若在极大项中出现的是命题变元，则标为0；若出现的是命题变元的否定形式，则标为1。这与极小项的标法相反。在二位二进制数与二位极大项之间同样存在一一对应。
三个命题变元的极大项是：
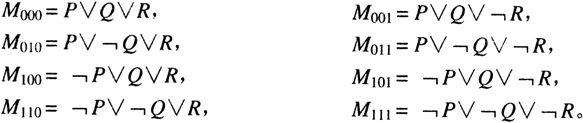
三个命题变元的极大项的下标是三位二进制数，它们与三位极大项也一一对应。一般，n位二进制数与n位极小（大）项之间一一对应。
极小项和极大项具有下列重要性质：
性质1．当且仅当对变元的真值指派与极小项脚标的编码相同时极小项取真值T。
性质1′．当且仅当对变元的真值指派与极大项脚标的编码相同时极大项取真值F。
性质2．不同极小项的合取是永假式。
性质2．′不同极大项的析取是永真式。
性质3．全体极小项的析取是永真式。
性质3．′全体极大项的合取是永假式。
性质4．下标相同的极小项和极大项互否。
此处关于极小项与关于极大项的性质是对偶给出的。而且性质2和3是性质1的直接推论。
性质1说，含有n个命题变元的2
n
个极小项中的每一个，它作为一个命题形式，其真值表中有且仅有一行取值T，其他2
n
－1行取值都为F。使其取值为T的是对n个命题变元的2
n
个指派中与该小项下标编码相同的那一个。性质1′说，含有n个命题变元的2
n
个极大项中的每一个，它作为一个命题形式，其真值表中有且仅有一行取值为F，其他2
n
－1行取值都为T。使其取值为F的是对n个命题变元的2
n
个指派中与该极大项下标编码相同的那一个。含有n个命题变元的真值函数，对n个命题变元的2
n
个指派，其取值是唯一确定的。对其取值为T的行，对应取极小项，然后将它们做析取，就得到了该真值函数的主析取范式。如果真值函数是重言式，其结果就是性质3；如果真值函数是矛盾式，其主析取范式是不含任一极小项的空式。对真值函数取值为F的行，对应取极大项，然后将它们做合取，就得到了该真值函数的主合取范式，如果真值函数是矛盾式，其结果就是性质3′；如果真值函数是重言式，其主合取范式是不含任一极大项的空式。含有n个命题变元的不同真值函数共有
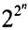个，含有n个命题变元的极小项和极大项都有2
n
个。对于每个极小项或极大项，它们被取和不被取，以构成主析取范式或主合取范式，不同的主析取范式或主合取范式有
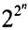个。可见，含有n个命题变元的真值函数与主析取范式或主合取范式一一对应。一个命题公式代表一个真值函数，有一个主析取范式且有一个主合取范式；反过来，一个主范式以其规范或标准形式代表一个真值函数，代表一类命题公式，真值函数与它的主析取范式或主合取范式相互唯一确定。给出一个真值函数的主范式，从主范式的形式结构很容易看出该真值函数的真值取值情况，对这一真值函数所代表的一类命题公式的判定便得以解决。主范式展现真值函数的取值，主范式的形式结构显示它的真值函数的特征。
求取任意一个命题公式的主范式有两种方法：等值推演法和真值表法。
1．等值推演法
【例1.8.2】 （P∧（Q↔R））∨﹁（P∨Q∨R）
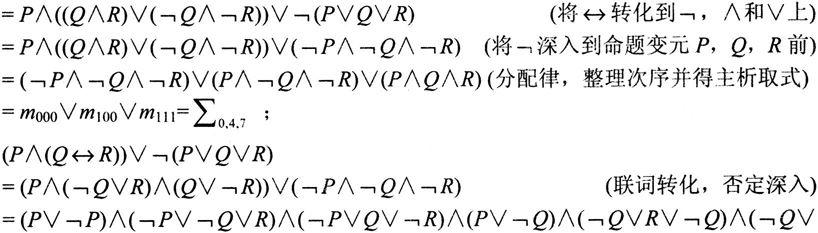
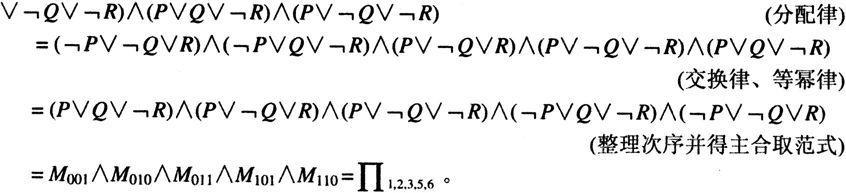
通过上述例子，总结使用等值推演方法求取主范式的步骤如下：
（1）将所给命题公式化归到﹁，∧和∨上；
（2）将﹁置命题变元前；
（3）利用交换、结合和分配律，先求析取范式或合取范式，并且利用零壹律删去含有互否文字的简单析取项或简单合取项；
（4）利用等幂律和吸收律，合并重复项或多余项；
（5）利用壹律，在求主析取范式的析取项中补入所缺少的文字
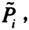补入方法是：（…∧（P
i
∨﹁P
i
））；在求主合取范式的合取项中补入所缺少的文字P
i
，补入的方法是：（…∨（P
i
∧﹁P
i
））；
（6）再经分配律、交换律和等幂律合并并按命题变元字母顺序整理便得与原公式等值的主范式。
在上述例子中，注意到这样一个事实：命题公式
（P∧（Q↔R））∨﹁（P∨Q∨R）
的主析取范式为：m 000 ∨m 100 ∨m 111 ＝∑ 0，4，7 ；主合取范式是：M 001 ∧M 010 ∧M 011 ∧M 101 ∧M 110 ==∏ 1，2，3，5，6 。
三位二进制编码共有8个，在主析取范式中出现了3个，其余5个恰好都出现在主合取范式中，并且不多也不少。在把二进制数转换为十进制数，以连乘号∏表记主合取，以连加号∑表记主析取，那么从
（P∧（Q↔R））∨﹁（P∨Q∨R）＝∑ 0，4，7 ＝∏ 1，2，3，5，6
可总结得到结论“命题公式主范式，析合结构两相依；编号不在极小（大）项，必定都在极大（小）项”。
到此，对于任一命题公式，只要求得它的一种主范式，利用该结论，就可以得到另一种主范式。
2．真值表法
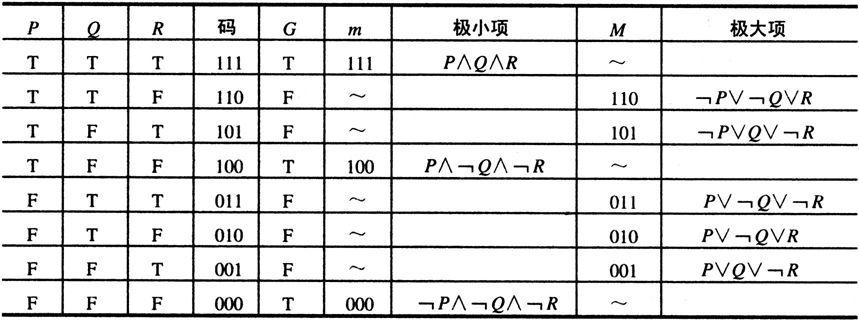
利用真值表法，求取命题公式的主范式，见表1-15（表中G＝（P∧（Q↔R））∨﹁（P∨Q∨R））为例，可将求取步骤归纳如下：
（1）给出要求主范式命题公式的真值表。
（2）在命题变元（P，Q，R）的真值指派栏内，看T为1，看F为0，得极小项m和极大项M的二进制编码。
（3）在命题公式真值栏内：见真（T）取极小项，取法是：相应于命题公式取真的编码，见1取变元，见0取否定；见假（F）取极大项，取法是：相应于命题公式取假的编码，见1取否定，见0取变元。
表1-15 利用真值法
（4）将取到的极小项作析取得主析取范式，将取到的极大项作合取得主合取范式：
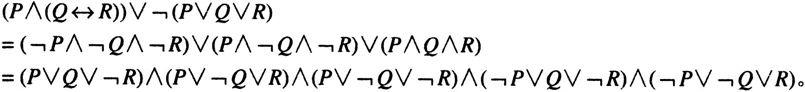
这与等价推演的结果完全一样。所以这样求取，其依据是有相同真值表的命题公式等值。其等值性，由极小项和极大项的性质以及逻辑联词∨和∧的定义，是显而易见的。
从真值表中，是否看到由一种主范式求另一种主范式的其他方法呢？下面介绍一种通过求主析取范式而演算出主合取范式的方法。
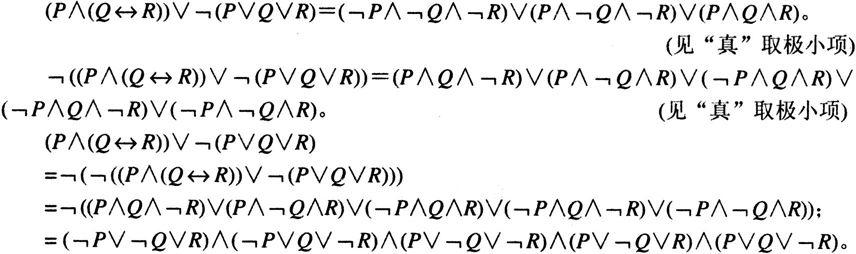
整理次序后，便是前面求得的主合取范式了。它是由取命题公式的否定式的主析取范式再否定而得到的。
一个命题公式是重言式，当且仅当它的主析取范式尽含全部极小项；一个命题公式是矛盾式，当且仅当它的主合取范式尽含全部极大项；不是上述两种情况的命题公式，是非重言式的可满足式。两个命题公式等值，当且仅当它们有相同的主范式。这些事实，从本节的讨论中可以总结和推论得到。
练习1-8
（1）写出下列含有4个命题变元的布尔项（脚标是十进制数）：
①m 10 ； ②M 10 ； ③﹁m 12 ； ④﹁M 12 。
（2）填空：
①m 110 ∧M 110 ＝（ ），m 110 ∨M 110 ＝（ ）；
②m 110 ∧m 011 ＝（ ），M 110 ∨M 011 ＝（ ）；
③命题公式G（P，Q，R）的主合取范式是∏ 0，1，5 ，它的主析取范式是（ ）；
④在对P，Q，R的真值指派TTF下，极小项m 010 取值为（ ），极大项M 001 取值为（ ）；
⑤
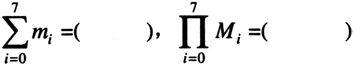（这里的m
i
与M
i
分别是P，Q，R的极大项和极小项而i是十进制数）；
⑥命题公式G的主合取范式是（P∨﹁Q），命题公式﹁G的主合取范式是（ ），命题公式﹁G的主析取范式是（ ）。
（3）求下列命题公式的合取范式和析取范式：
①（P∧（Q→R））→S；
②﹁（P∨Q）↔（P∧Q）。
（4）求下列命题公式的主范式：
①P→（（P→Q）∧（Q∧P））；
②Q∧（P∨﹁R）。
（5）判定下列命题公式（即指出所给命题公式是恒真式、恒假式、还是一般可满足式）：
①P→（P∧（Q→P））；
②（Q→P）∧（﹁P∧Q）；
③（﹁P∨﹁Q）→（P↔﹁Q）；
④P∧（P→Q）→Q。
