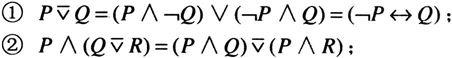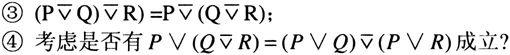下载掌阅APP，畅读海量书库
立即打开
逻辑联词﹁、∨、∧、→和↔是逻辑演算中最常用到的5个逻辑联词。为了某种特别应用的需要，在命题逻辑中还定义了其他的逻辑联词。下面介绍其中的3个。
1．异或
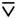
异或，
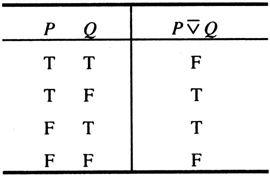
即不可兼的或。这种“或”取真时不承认构成“或”的两个支命题可同时取真。其真值表是（见表1-11）。
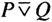取真值真当且仅当P与Q的真值取值不相同。与可兼的或∨不同的是：P与Q同取真值T时，P∨Q取值为T而
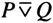取值为F。对照双条件命题的真值表，显然有：
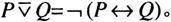
表1-11 异或真值表
通过构造真值表，容易证明关于“异或”的下述运算性质。
（1）
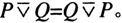
（2）
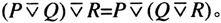
（3）
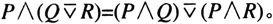
（4）
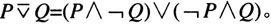
（5）
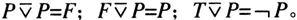
（6）若
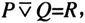则
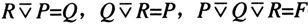（其中P，Q，R是任意命题公式）。
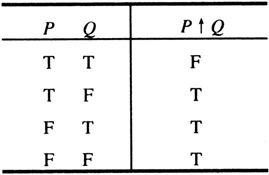
2．与非（↑）
命题P与Q的与非是命题P↑Q，读作P与非Q。P↑Q取值假，当且仅当P与Q同取真值真。从真值表（见表1-12）易见：P↑Q＝﹁（P∧Q）。
表1-12 与非真值表
在逻辑联词与非↑上，成立以下联词转化律：
（1）﹁P＝﹁（P∧P）＝P↑P。
（2）P∧Q＝﹁（﹁（P∧Q））＝﹁（P↑Q）＝（P↑Q）↑（P↑Q）。
（3）P∨Q＝﹁（﹁P∧﹁Q）＝﹁P↑﹁Q＝（P↑P）↑（Q↑Q）。
3．或非（↓）
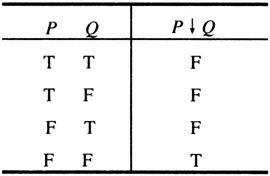
命题P与Q的或非是命题P↓Q，读作P或非Q。P↓Q取值为真，当且仅当P与Q同取值假。从真值表（见表1-13）易见：P↓Q＝﹁（P∨Q）。
在逻辑联词或非↓上，成立以下联词转化律：
（1）﹁P＝﹁（P∨P）＝P↓P。
（2）P∨Q＝﹁（﹁（P∨Q））＝﹁（P↓Q）＝（P↓Q）↓（P↓Q）。
（3）P∧Q＝﹁（﹁P∨﹁Q）＝﹁P↓﹁Q＝（P↓P）↓（Q↓Q）。
表1-13 或非真值表
逻辑联词﹁、∨、∧，都可由与非“↑”和或非“↓”予以等值表达。那→和↔是否也能如此呢？从
P→Q＝﹁P∨Q＝﹁（P∧﹁Q）＝P↑﹁Q＝P↑（Q↑Q）
看到P→Q也可由与非“↑”等值表达。
其实，P→Q＝﹁P∨Q，而P↔Q＝（P→Q）∧（Q→P），只要将→、↔通过上式在﹁、∨与∧上首先作等值化，然后再用“与非”和“或非”的联词转化律，便可完成由↑或↓对→和↔的等值表达。
在作上述讨论后，读者自然要问，是否还需要其他的逻辑联词？既然逻辑联词可以相互表达，那么怎样的逻辑联词组含有最少的逻辑联词，但可以表达所有的逻辑联词？第一个问题我们留作练习，第二个问题即我们要引入的概念：逻辑联词的完备集。
使用逻辑联词↑（或↓），可以等值表出含有逻辑联词﹁，∨，∧，→和↔的所有命题公式，它们虽然是由一个逻辑联词组成的逻辑联词集｛↑｝（或｛↑｝），但“功能完备”，是一个逻辑联词的完备集。
所谓逻辑联词的完备集是这样的一个逻辑联词的集合，它可以等值转化含有任一逻辑联词的命题公式，如若减少集合中的逻辑联词，则丧失此性质。
逻辑联词集｛﹁，∨｝，｛﹁，∧｝，｛﹁，→｝，｛↑｝和｛↓｝都是逻辑联词完备集。
实际上，除了已经讨论的﹁，∨，∧，→，↔，
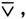↑和↓这八个逻辑联词外，还有一个逻辑联词，即条件否定。命题P和Q组成条件否定命题P↦Q，读作并非若P则Q。P↦Q取值真，当且仅当P取真值真而Q取值假，即：P↦Q＝﹁（P→Q）。
在逻辑演算中，并不需要这么多的逻辑联词，一般有两个就足够了，其他几个可以由它们来定义。所选用的两个逻辑联词构成逻辑联词的完备集，称它们为初始逻辑联词。如，当选用﹁，→为初始逻辑联词时，∧、∨和↔可以这样定义：
P∧Q＝ df ﹁（P→﹁Q）
P∨Q＝ df ﹁P→Q
P↔Q＝ df ﹁（（P→Q）→﹁（Q→P））
初始逻辑联词是逻辑演算形式系统的初始符号。
在电子计算机的逻辑设计中使用逻辑联词↑和↓。理论上讲，它们的每一个都可以单独选用为初始逻辑联词，但一般不采用一个逻辑联词作为初始联词符号，因为那样会使表达式冗长且不易阅读。
当一个由两个逻辑联词组成的完备集被用以逻辑系统的初始逻辑联词时，其他的逻辑联词用定义给出，在使用时这些逻辑联词被看作是表达它们的初始逻辑联词符号串的缩写。在逻辑系统中，﹁、∨、∧、→和↔这5个逻辑联词都使用，当﹁，→作为初始逻辑联词时，系统中的P∧Q，P∨Q和P↔Q被分别视为是﹁（P→﹁Q），﹁P→Q和﹁（（P→Q）→﹁（Q→P））的缩写。
练习1-6
（1）在逻辑联词完备集｛﹁，∨｝上等值表达下列各命题公式。
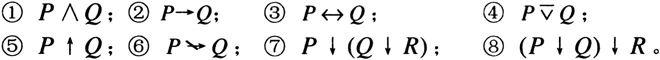
（2）证明：
①↑和↓具有逻辑运算交换律，即证：P↑Q＝Q↑P，P↓Q＝Q↓P；
②↑和↓不具有逻辑运算结合律，即证：一般P↑（Q↑R）≠（P↑Q）↑R；P↓（Q↓R）≠（P↓Q）↓R。
（3）在逻辑联词完备集｛↓｝上等值表达下列各命题公式
①P→Q；②P↑Q；③P↔Q；④P
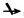Q。
（4）在下列真值表表头括号中填上适当的逻辑联词：
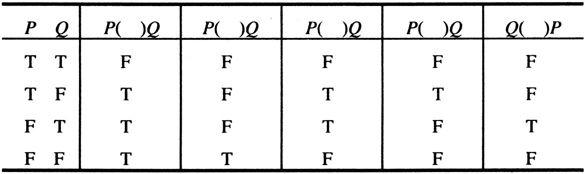
（5）通过对已定义的9个逻辑联词和练习1-3中练习题（4）的分析，能否说，命题逻辑的逻辑联词也只须定义这9个了？
（6）证明并考虑：
