




永真公式称重言式,永假公式称矛盾式,不是矛盾式的命题公式称可满足式。命题逻辑中数量无限的命题形式仅此而已。重言式是我们特别感兴趣的,因为它反映的是命题逻辑中的逻辑规律。例如重言式的合取式还是重言式。命题公式G是重言式,无论它所含的命题变元指真还是指假,G都取真值T。因此,在G中,将其所含某变元都以同一命题公式作代入,所得的命题公式G′还是重言式。换句话说,决定命题公式是重言式的是命题公式自己的形式结构,而不是它含有多少或怎样的命题变元。如,P∨﹁P是重言式;((Q∨R)→S)∨﹁((Q∨R)→S)一样还是重言式。因为“~∨﹁~”的形式结构是重言式形式结构。P∨﹁P所反映的逻辑规律即排中律。
命题公式A与B等值,在它们所含命题变元的任何指派下,A与B都有相同的真值,于是由A和B构成的双条件命题A↔B是重言式;反过来,若A↔B是重言式,则在对A、B所含命题变元的所有指派下,A、B的真值取值都相同,从而A=B。可见A与B等值,当且仅当A↔B是重言式。
一个类似的讨论是:A→B是重言式,当且仅当A⇒B。这里A⇒B读作A蕴涵B。A蕴涵B,当且仅当A→B是重言式,即当且仅当A取真值T时,B必取真值T;或者当且仅当B取值F时,A必取值F。这样分析的重要性在于:它依此可以作为证明一个命题公式蕴涵另一个命题公式的方法。
例如对(1)P⇒P∨Q;(2)P∧Q⇒P的证明,就可以这样做:
(1)当前件P取真值T时,则后件P∨Q=T∨Q也必取真值T。因而,P→P∨Q是重言式。故P⇒P∨Q。
(2)当后件P取真值F时,则前件P∧Q=F∧Q也必取真值F。因而,P∧Q→P是重言式。故P∧Q⇒P。
一个正确的逻辑推理形式,由真的前提出发必能得出真的结论,其前提与结论之间的逻辑形式正是蕴涵式。如果推理形式是正确的,那么由推理的前提和结论构成的条件公式必定是一个重言式。检查一个推理的推理形式是否正确,只须写出相应于推理的条件命题公式,判定这个条件命题公式是否重言式即可。
使用此方法,可以证明下述基本蕴涵式。
(1)化简式:P∧Q⇒P;P∧Q⇒Q。
(2)附加式:P⇒P∨Q;Q⇒P∨Q。
(3)假言推理:P∧(P→Q)⇒Q。
(4)拒取式:﹁Q∧(P→Q)⇒﹁P。
(5)析取三段论:﹁P∧(P∨Q)⇒Q。
(6)假言三段论:(P→Q)∧(Q→R)⇒P→R。
(7)二难推论:(P∨Q)∧(P→R)∧(Q→S)⇒R∨S。
(8)等价三段论:(P↔Q)∧(Q↔R)⇒(P↔R)。
(9)合成式:P,Q⇒P∧Q(此式的逻辑含义是:有前提P,Q可得结论P∧Q)。
这些基本蕴涵式,反映了命题逻辑推理的形式结构,体现了基本的逻辑规律,总结了人们思维推理的一些常用方法,并且是证明其他推理形式的基础和依据。
【例1.5.1】 逻辑推理的一个具体例子:
若a>0,则|a|=a
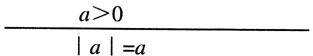
其形式结构即假言推理。
【例1.5.2】 由基本蕴涵式证明:
(1)﹁P⇒P→Q;(2)﹁(P→Q)⇒P。
证明:(1)由附加式,﹁P⇒﹁P∨Q知﹁P→(﹁P∨Q)是重言式。做等值替换得重言式﹁P→(P→Q),所以﹁P⇒P→Q。
(2)由化简式P∧﹁Q⇒P知,(P∧﹁Q)→P是重言式,而P∧﹁Q=﹁(﹁P∨Q)=﹁(P→Q),所以﹁(P→Q)→P是重言式,即﹁(P→Q)⇒P。
【例1.5.3】 使用归谬法证明(P→Q)→(﹁Q→﹁P)是重言式。
假定(P→Q)取值T,而(﹁Q→﹁P)取值F(即(P→Q)→(﹁Q→﹁P)并非重言式)。于是﹁Q值为T,而﹁P值为F,即Q值为F,P值为T,因而P→Q取值F。这与(P→Q)取值T矛盾。所以(P→Q)取值T时(﹁Q→﹁P)只能取值T,故(P→Q)→(﹁Q→﹁P)是重言式。同样方法还可以证明(﹁P→﹁Q)→(Q→P)也是重言式。
【例1.5.4】 一个数学推理的逻辑形式结构正确性的证明。
数学命题“若a 2 是偶数,则a是偶数”的证明可以用归谬法作以下推演。
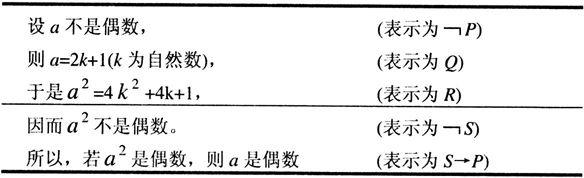
上述证明的推理形式是:﹁P→Q,Q→R,R→﹁S,所以S→P。此推理形式即:
﹁P→Q,Q→R,R→﹁S⇒S→P。
要证明这一数学推理的抽象的逻辑推理形式是正确的,现在只须证明(﹁P→Q)∧(Q→R)∧(R→﹁S)→(S→P)是重言式。下面给出3种证明G=(﹁P→Q)∧(Q→R)∧(R→﹁S)→(S→P)是重言式的证明方法。
(1)真值表法(见表1-10)
表1-10 真值表
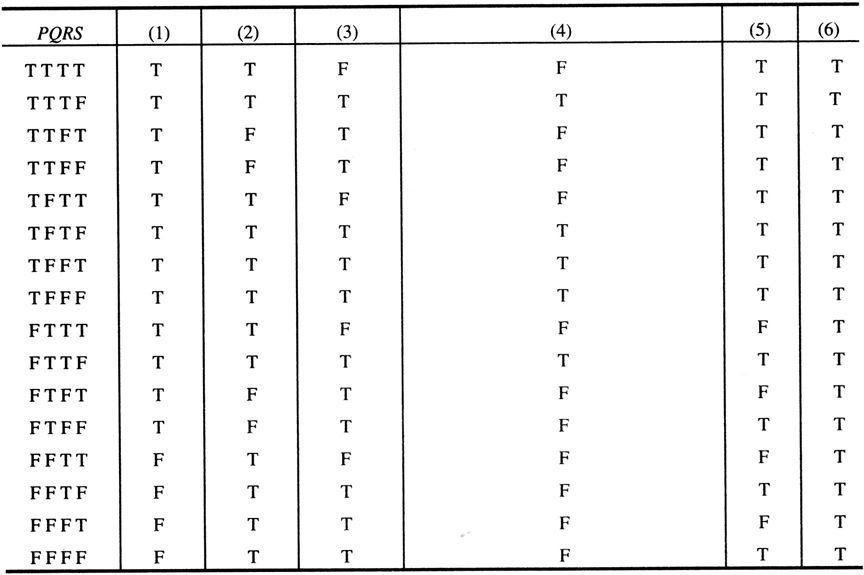
表中第2列是﹁P→Q的真值表,第3列是Q→R的真值表,第4列是R→﹁S的真值表,第5列是(﹁P→Q)∧(Q→R)∧(R→﹁S)的真值表,第6列是S→P的真值表,第7列是公式G的真值表。从表1.10的真值表可知(﹁P→Q)∧(Q→R)∧(R→﹁S)→(S→P)是重言式,因而有﹁P→Q,Q→R,R→﹁S⇒S→P。
(2)等值推演法

(3)简化真值表法
用简化真值表法证明条件命题公式A→B是重言式,只须证明当A取T值时B也取T值;或者当B取F值时,A也取F值。不然,则A→B非重言式。
在G中,假定S→P取值F,则S取值为T,而P取值为F。于是﹁P取值是T,而﹁S取值是F。考虑﹁P→Q,R→﹁S和Q→R。若Q→R为假,则(﹁P→Q)∧(Q→R)∧(R→﹁S)取值为F,因而G是重言式得证。若Q→R取值真,则要么Q、R同真,要么Q取值为假。若是前者,则R→﹁S取值假;若是后者,则﹁P→Q取值假。不管是哪种情况,都有(﹁P→Q)∧(Q→R)⋀(R→﹁S)取值为F,因而G是重言式。综上所述可知(﹁P→Q)⋀(Q→R)∧(R→﹁S)→(S→P)是重言式。
下面讨论等价与蕴涵的关系。
设A,B是命题公式,则A=B当且仅当A↔B是重言式。但A↔B=(A→B)∧(B→A)。因而当且仅当(A→B)∧(B→A)是重言式。因此,当且仅当(A→B)且(B→A)是重言式。于是当且仅当A⇒B且B⇒A。可见证明两个命题公式等值,当且仅当证明这两个命题公式互蕴涵。
蕴涵有如下重要性质:
(1)设A,B,C是命题公式,则如果A⇒B且A⇒C,那么A⇒B∧C。
事实上,由A⇒B,A⇒C可知A→B及A→C都是重言式。因而当A取真值T时,B、C必都取得真值T,从而B∧C取得真值T,于是A→B∧C是重言式,即A⇒B∧C。
同理可得:若A⇒C且B⇒C,则A∧B⇒C及若A⇒C且B⇒D则A∧B⇒C∧D。
(2)设A,B,C是命题公式,则如果A⇒C且B⇒C那么A∨B⇒C。
这是因为,C取真值F时,由A⇒C,B⇒C知,A,B都取真值F,于是A∨B也取真值F,所以A∨B⇒C。
练习1-5
(1)设P→Q为条件命题,则称﹁P→﹁Q,Q→P和﹁Q→﹁P分别为P→Q的否定式,逆换式和逆否式。试写出命题:“如果你能持之以恒,那么就会自学成才”的否定式、逆换式和逆否式,并分析它们与条件命题P→Q之间的真值取值关系。
(2)证明:
①若A⇒C且B⇒D,则A∧B⇒C∧D。
②若A⇒B且B⇒C,则A⇒C。
(3)判断下列命题的真伪:
①重言式的否定式是矛盾式。
②矛盾式的否定式是重言式。
③不是重言式,就是矛盾式。
④不是矛盾式,就是重言式。
⑤重言式必为可满足式。
⑥不是矛盾式,就是可满足式。
⑦可满足式未必是重言式。
⑧不是可满足式就是矛盾式。
(4)请将元人姚燧的诗“欲寄君衣君不还,不寄君衣君又寒;寄与不寄间,妾身千万难”写成命题形式。


