1.4　真值表与等值公式

设含有n个不同的命题变元P ₁ ，P ₂ ，…，P _n 的命题公式是G（P ₁ ，P ₂ ，…，P _n ），对这n个变元的所有不同的真值指派，G都有相应的真值取值。称由命题变元指派真值，命题公式对应取值列成的一张表为真值表。含有n个相异命题变元的命题公式，其真值表有2 ⁿ 个指派行。

表1-8是命题公式（1）P∧﹁P；（2）Q∨﹁Q；（3）P→Q；（4）﹁P∨Q的真值表。

表1-8　真值表

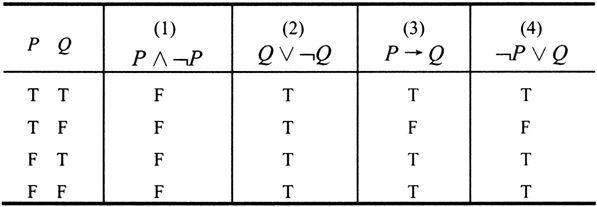
不论其所含命题变元取何种指派，其真值永为真的命题公式称永真式，记为T，如（2）；其真值永为假的命题公式称永假式，记为F，如（1）。像（3）和（4），对于它们所含命题变元的全部真值指派，都有相同（对于每一指派）的真值取值，这样的命题公式称作逻辑等值式或等值公式。这里约定：将A与B等值就记为：A＝B（式中的A，B是命题公式）。

通过构造真值表，容易证明下述12组基本等值式，它们是命题逻辑等值演绎的12组运算定律。

（1）对合律　﹁（﹁P）＝P

（2）幂等律　P∧P＝P；P∨P＝P

（3）结合律　（P∧Q）∧R＝P∧（Q∧R）；（P∨Q）∨R＝P∨（Q∨R）

（4）交换律　P∧Q＝Q∧P；P∨Q＝Q∨P

（5）分配律　P∧（Q∨R）＝（P∧Q）∨（P∧R）；P∨（Q∧R）＝（P∨Q）∧（P∨R）

（6）吸收律　P∧（P∨Q）＝P；P∨（P∧Q）＝P

（7）反演律　﹁（P∧Q）＝﹁P∨﹁Q；﹁（P∨Q）＝﹁P∧﹁Q

（8）壹律　　P∧T＝P；P∨F＝P

（9）零律　　P∧F＝F；P∨T＝T

（10）矛盾律　﹁（P∧﹁P）＝T

（11）排中律　P∨﹁P＝T

（12）联词转化律　P→Q＝﹁P∨Q；P↔Q＝（P→Q）∧（Q→P）

在复合命题公式中，其分子公式（必须也是命题公式）可以用与其等值的命题公式替换。替换后所得的新公式与原公式逻辑等值。这一事实称为替换原理。使用替换原理被替换掉的是子公式，并不必须是命题变元，而且也未必对复合命题公式中的同一子公式的每一出现都做替换。替换原理与练习1.3中所讲代入原理是有区别的。

利用运算定律和替换原理，可以进行命题公式间的等值推演，称命题演算见表1-9。

表1-9　命题演算示例

表1-9所示示例是一个等值推演。在上述命题演算下，并未使用真值表，也证明了公式P→（Q→R）与Q→（P→R）逻辑等值。

练习1-4

（1）构造下列命题公式的真值表：

①（P→（Q→R））→（（P→Q）→（P→R））；

②（﹁P∨Q）∧（P∨﹁Q）；

③（P∧Q）∨（﹁P∧﹁Q）；

④﹁（P↔Q）↔（﹁P↔Q）。

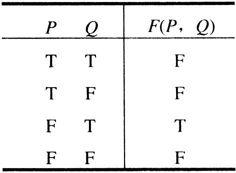
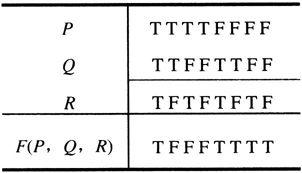
（2）设命题形式的真值表如下表，求出一个具有下列真值表的尽量简单的命题公式：

（3）用等值推演法证明永真式：

①P→（Q→P）；

②﹁P→（P→Q）；

③（﹁P→﹁Q）→（Q→P）；

④（P→Q）→（P→（Q∨R））。

（4）下列判断（命题）是否正确（真）？式中A，B，C是任意命题公式。

①若A∧C＝B∧C，则A＝B；

②若A∨C＝B∨C，则A＝B；

③若A∧C＝B∧C且A∨C＝B∨C，则A＝B；

④若﹁A＝﹁B，则A＝B；

⑤若A→B是永真式，则﹁B→﹁A是永真式。 TckmZxi0UptrJSSA9eoeuq/AH1GwdUeWqvjWcYK9BEZn3t7sGOgXzXziT0yy72V5