





知名作家圣彼得·伯南丁曾说过他小时候关于地球与太空的奇怪想法。他认为,从表面上看,太阳是从一座山的背后升起来,再从另一座山落下去。他觉得天空就像一座蓝色的拱桥,或者像一个倒扣在地球边缘的碗。他想象着,为了不碰到头,他必须弯着腰行走才能达到地球的边缘。有一天,为了解除困惑,他决定去证实这一切。于是他准备了一些吃的东西,然后就出发了。他走啊走啊,走了好长时间,只希望可以快点亲手触摸到天空;可是这座拱桥在他前进的过程中却在不断地后退,好像永远都走不到尽头。最后他走得实在太累了,于是放弃了这次探险。但是,即使他沿原路返回了,他还是相信天空就是一座大拱桥,这样的话,那到达不了、摸不到它就很好解释了:他的腿不够长,力量不够大,所以怎样也无法碰到天空。
我亲爱的读者们,小时候你们应该也有过这种幼稚的想法吧:认为地球就是一片无限延伸的被蓝色的穹顶所包围的广阔土地,只是中间被山脉切割。但是现在我们清楚地知道:天空没有任何一个角落是与地面相接的,地面上也没有任何一个地方是可以触碰到天空的,因为任何地方的天空的高度都是一样的。我们也知道:当我们直直地向前走时,会看到平原、山脉、海,却永远都无法走到地球的边缘。简单来说,地球是圆的。如果我们朝着一个方向一直走,最后我们还是会回到原点。
地球是漂浮在太空中的一个巨大的球体。假设在空中有一个用绳子系着的大球,球面上有一只昆虫。假如这只昆虫想要从球的一边爬到另一边,那么它肯定可以顺利做到,途中不会遇到什么障碍物,也不会有突起的障碍阻碍它前进。这与在地球上的我们是一样的,即使比起这只昆虫,地球上的我们显得渺小很多。我们从无数个不同的方向来来去去,未曾遇到过障碍物,也未曾触碰到天空,完成了最遥远的旅程,甚至是环球之旅,最后又返回到起点。照这么看来,地球就应该是圆的,是漂浮在太空中的一个巨大的球体。至于头顶上那个蓝色的穹顶,只不过是地球表面的空气折射形成的蓝色光线。
以下事实可以用来证明地球是圆的。有一名旅行者在去往一个小镇的途中经过一片很平坦的平原,在平原上没有任何事物会挡住他的视线,站在某个地方,他首先看到的就是小镇的最高处——尖塔的最高点。站在近一点的地方,才可以看见尖塔的整个顶部,然后是屋顶,最后才能看到整个建筑物。所以,随着距离远近的变换,我们首先看到的都是物体的最高点,最后看到的是最低点。假如地球是平的,那么就不是这样的了。站在任何一个地方,我们都可以直接看到塔的全身,而不是先看到顶部,然后再是底端。如图1所示,在塔的右侧,不论是站在A点还是B点,都可以直接看到塔的全身。另外,假如地球是圆的,那么远处的物体就会因为地球表面弯曲而被挡住,就像我们之前所讲的那样,物体将会从顶点开始慢慢出现在我们眼前。因此,如图2所示,站在A点的话,是根本看不到塔的,因为视线被地球弯曲的表面挡住了;站在B点,也只能看到塔的上半部分;而站在C点,就可以看到塔的全部了。

图1
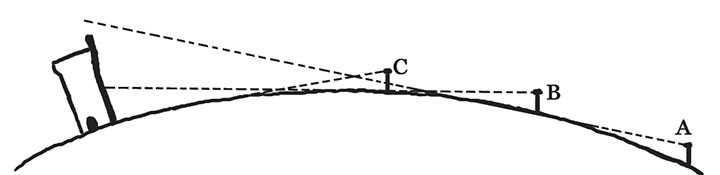
图2
在陆地上,很少有视野那样宽广同时又规则的观察点的,因为总是会有山脉以及数不清的植物干扰我们的视线,所以,任何塔或尖塔都是按照从顶部到底部的顺序慢慢映入我们眼帘的。而海面突起的表面是跟地球表面的弯曲度类似的,那么在没有障碍的海面上,就可以很好地解释地球是圆的这一事实了。
当一条船慢慢地向海岸靠近时,船上的人首先看到的是岸上建筑物的最高点,如山顶,接着是高塔的塔顶,然后才是海岸。同样,岸上人首先看到的是上桅杆,接着是中桅杆,然后是帆,最后才是船身。假如船是从海岸开走,那么如图3所示,这些物体消失的顺序将会与船开向海岸时的顺序相反,也就是说:首先消失在眼前的将会是船体,接着是帆,然后是中桅杆,最后才是上桅杆。
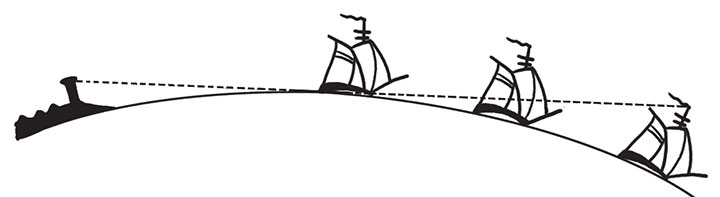
图3
地平线的形状也可以证明地球是圆的。“地平线”这个术语来源于希腊语,它的意思是“边界、界限”,用来指站在地面的某个地方,视野所及的范围。
地平线好像把天空和地面连接起来了。当观察者站在绝对平坦的地面上时,将会形成一个以他为中心的地平线圈。地平线的形状在海上表现得更明显,它就像一个巨大的圆盘与蓝天相接。假如地球是平的,就只有视力的好坏会影响到视野,而且用足够强大的望远镜就可以看得到任何距离的物体,那么地球上的事物就一览无余了。但是真实情况并不是这样的:即使用最好的望远镜,也是看不到地平线另外一端的物体的。这么看来,地球就不是平的,而是圆的。我们来看下图4,一切就清楚了。假设球面上方有一条垂线OB,我们从A点往球面看,那么可以看到的是哪部分呢?答案很简单。我们以A为起点画一条直切线AK,K点与球面相切,这条线表示的就是视线,所有在这条线和A点之间的范围的都是我们能看到的部分,而超出这范围的都是我们看不到的。如果,我们再以A点画与AK类似的AP、AQ、AR、AS等无数条直线,这些线的另一端都是落在球面上,那么所有落在球面上的这些点最后将会形成一个完整的圆。从OB线上的其他点画类似这样的线,也会得出同样的结果。这么说来,不管在哪个点,如果我们所看到的地平线是一个圆的话,那么地球一定是个球体。
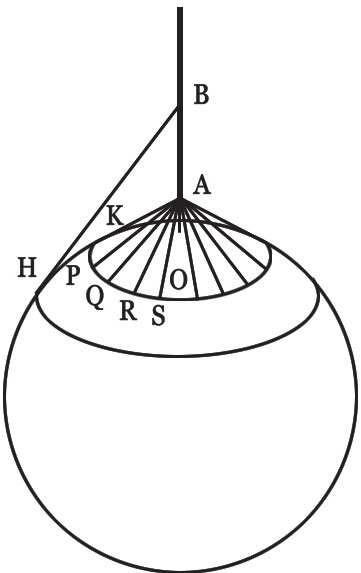
图4
这个被我们叫做地球的东西的周长有4万千米。接下来我会讲明这个数字所代表的意义。如果你曾经爬过塔,当站在塔上俯瞰周围的景色时,你一定被眼前那无限延伸的土地给震住了,而那蓝色的地平线好像真的很遥远,在记忆中,那就是最遥远的距离。地平线离我们到底有多远呢?从塔顶我们到底可以看到多远呢?这取决于两样东西,塔的高度和地面的凹凸程度。我们再来看下图4,假设观察点不是在A点,而是在高一点的B点,那么视线的另一端将能落在球面的更远处,假设那是H点,那么我们的视野就更宽了。所以,由于地球是圆的,我们站得越高,就看得越远。
另一方面,在多山脉的地方,由于地面凹凸不平,视野就会受到影响,地平线也同样会受到限制。假如把地面看成跟海平面一样的平坦,同时把观察点设在142米高的斯特拉斯堡教堂钟楼上,在这种情况下,地平线周长就是40千米。假如有另外一个圣彼得·伯南丁,他拥有强壮的双腿,那么只要花上一天的时间,他就可以走到从斯特拉斯堡教堂钟楼上所看到的地平线;如果他做到了,那么第二天他可能没有勇气,也没有力气再出发了。我们的地球是如此之大,它的周长是4万千米,是我们从斯特拉斯堡教堂钟楼上所看到的地平线周长的1万倍啊。
这时你肯定会问:地球上有那么多庞大的山脉和深谷,使得地球表面凹凸不平,那为什么还说地球的表面是圆的呢?你们更愿意相信海面是均匀的,而陆地则不是,因为我们所看到的陆地到处都是坑坑洼洼的。布满山脉、峡谷、平原以及悬崖峭壁的地球表面怎么会是规则的呢?我们怎么从这个极不规则的球面上找出它的规则呢?我反过来问你们:橘子是圆的吗?你肯定会回答:是的。尽管仔细观察就会发现橘子的表面是坑坑洼洼的,但是这些坑坑洼洼与它的大小比起来根本不算什么,所以橘子还是圆的;所以我也可以这样说,地球就是圆的,因为地球表面的这些很高的山脉与地球庞大的身体比起来根本不算什么。下面我会对此作出证明。
现在,我们用一个直径2米的表面光滑的球来代替地球,然后按照正确的比例,在它的表面标出一些主要的山脉。在这些山脉中,最高的是位于亚洲中部的珠穆朗玛峰,其海拔约8840米,直入云间,它的底部占据了非常大的空间,相当于一个帝国的面积。当这样的一座庞大的山出现在我们面前时,我们会做何感想呢?如果我们要让这座大山按正确的比例在我们假设的球上显示,你知道用什么来表示吗?一粒沙子,一粒直径只有1毫米多的沙子!如此看来,这样一座庞大的山与地球比起来根本就不算什么。就像橘子表面最小的疙瘩一样,对于橘子来说,也是可以忽略的。至于欧洲最高的山脉——勃朗峰,我们只要用一粒直径只有一半的沙子来表示就可以了,它的海拔约4810米。不需要再举更多的例子,球面有无数这样的沙子,而这些沙子就相当于地球上无数的山脉,尽管数量很多,但是丝毫不会影响球体的形状。也就是说,地球只不过是这个球的无限放大版。
那么地球是怎样平稳地悬浮在太空中的呢?它是不是被某种天体链吊起来的呢,就像宫殿顶部的圣灯一样?又或者有某个物体支撑着它,就像地球仪的底座一样?……很多旅者从不同的地方环行地球,但是都从未看见任何的吊链或者支撑物。每个地方都一样,他们都只看到陆地、天空和海洋。因此,我们可以断定:地球是一个独自悬浮在太空中的星球。
那么,为什么它不会掉下来呢?嗯,这是个关键问题!不过可以想一想,也许你就会知道为什么地球不会掉下来。你看到的是什么?广阔的天空、无边无际的空间。假如你站在地球的另一面,你会看到什么?还是广阔的天空、无边无际的空间。假如是站在分界线的左边或右边呢?还是一样。无论站在什么地方,都是看到广阔的天空以及无边无际的空间。现在请告诉我:在这无边无际的空间里,地球会从哪个地方掉下来呢?如果可以,请先告诉我,地球的哪边是上面?哪边是下面?这里的上面是指天空,不过请记住:无论在哪个地方,天空都是一样的。如果你很清楚地球不会落到我们头顶的天空,那么你为什么会觉得天空会落进我们脚下的“天空”呢?就像我们不会去怀疑地球会升到天空一样,我们也不要去怀疑地球会掉下来。
在下一章,我们将会对这个问题作进一步的讲解,我们会讲述物体掉落的原因。不过,我们先总结一下本章的要点:地球是球状的,而且是独立存在于太空中的。它的周长是4万千米。它的半径,也就是从球心到表面的距离是6366千米。地球表面的庞大物体,对于地球来说根本就微不足道,并不会对地球的形状造成任何的影响。